一、关键路径
1.1 网络
- AOV网络:有向图,用顶点表示活动,用弧表示活动的先后顺序
- AOE网络:有向图,用顶点表示事件,用弧表示活动,用权值表示活动消耗时间
1.2 名词解释
活动:业务逻辑中的行为,用边表示
事件:活动的结果或者触发条件
关键路径:具有最大路径长度(权重)的路径,可能不止一条
活动的两个属性:
- e(i)表示最早开始时间
- l(i)表示最晚开始时间
事件的两个属性:
- ve(j)最早开始时间
- vl(j)最晚开始时间
在下面的计算过程中,就可以理解这些属性的概念了
二、计算关键路径的过程
原理:
- 先求出每个顶点的ve和vl值
- 通过这两个值就可以求出每条边的e和l值。
- 取e(i)=l(i)的边就是
关键路径上的边,关键路径不止一条
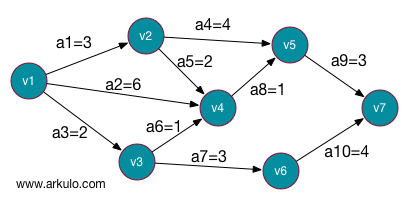
2.1 求ve(i)的值
- 从前向后,直接前驱节点的ve值+当前节点的边的权值(有可能多条,取最大值)
- 第一个顶点的ve等于0
- ve(1) = 0
- ve(2) = ve(1) + len(a1) = 0 + 3 = 3
- ve(3) = ve(1) + len(a3) = 0 + 2 = 2
- ve(4) = ve(1) + len(a2) = 0 + 6 = 6
- ve(5) = min{ve(2) + len(a4),ve(4) + len(a8)} = max{7,7} = 7
- ve(6) = ve(3) + len(a7) = 2 + 3 = 5
- ve(7) = min{ve(a5) + len(a9),ve(6) + len(a10)} = max{10,9} = 10
下表为各顶点(事件)的ve值:
| 顶点 | ve(1) | ve(2) | ve(3) | ve(4) | ve(5) | ve(6) | ve(7) |
|---|---|---|---|---|---|---|---|
| ve(i) | 0 | 3 | 2 | 6 | 7 | 5 | 10 |

2.2 求vl(j)的值
- 从后向前,直接后继节点的vl值-当前节点的边的权值(有可能多条,取最小值)
- 终结点的vl等于它的ve
- vl(7) = ve(7) = 10
- vl(6) = vl(7) - len(a10) = 10 - 4 = 6
- vl(5) = vl(7) - len(a9) = 10 - 3 = 7
- vl(4) = vl(5) - len(a8) = 7 - 1 = 6
- vl(3) = min{
vl(6) - len(a7),vl(4) - len(a6)} = min{3,5} = 3 - vl(2) = min{
vl(5) - len(a4),vl(4) - len(a5)} = {3,4} = 3 - vl(1) = min{
vl(2) - len(a1),vl(4) - len(a2),vl(3) - len(a3)} = min{0,0,1} = 0
下表为各顶点(事件)的vl值:
| 顶点 | vl(1) | vl(2) | vl(3) | vl(4) | vl(5) | vl(6) | vl(7) |
|---|---|---|---|---|---|---|---|
| vl(j) | 0 | 3 | 3 | 6 | 7 | 6 | 10 |

2.3 求e(i)的值
e(i):活动ai是由弧边(活动)的最早开始时间等于它发出的顶点(事件)的的最早发生时间
参考之前的个顶点的ve和c:
| 顶点 | ve | vl |
|---|---|---|
| v1 | 0 | 0 |
| v2 | 3 | 3 |
| v3 | 2 | 3 |
| v4 | 6 | 6 |
| v5 | 7 | 7 |
| v6 | 5 | 6 |
| v7 | 10 | 10 |
- e(1)、e(2)、e(3) 活动(a1、a2、a3三条边)发出的顶点为v1,时间为0
- e(4) 即为
a4这条边发出的顶点v2的发生的时间ve(2)= 3 - e(5) 即为
a5这条边发出的顶点v2的发生的时间ve(2)= 3 - e(6) 即为
a6这条边发出的顶点v3的发生的时间ve(3)= 2 - e(7) 即为
a7这条边发出的顶点v3的发生的时间ve(3)= 2 - e(8) 即为
a8这条边发出的顶点v4的发生的时间ve(4)= 6 - e(9) 即为
a9这条边发出的顶点v5的发生的时间ve(5)= 7 - e(10) 即为
a10这条边发出的顶点v6的发生的时间ve(6)= 5
得出的e(i)值:
| 边 | a1(3) | a2(6) | a3(2) | a4(4) | a5(2) | a6(1) | a7(3) | a8(1) | a9(3) | a10(4) |
|---|---|---|---|---|---|---|---|---|---|---|
| e(i) | 0 | 0 | 0 | 3 | 3 | 2 | 2 | 6 | 7 | 5 |

2.4 求l(i)的值
l(i):活动ai是由弧
参考之前的个顶点的ve和c:
| 顶点 | ve | vl |
|---|---|---|
| v1 | 0 | 0 |
| v2 | 3 | 3 |
| v3 | 2 | 3 |
| v4 | 6 | 6 |
| v5 | 7 | 7 |
| v6 | 5 | 6 |
| v7 | 10 | 10 |
l(i) = 当前边的指向结点的最晚发生时间[vl(i)] - 当前时间(即边)所消耗的时间
- l(1) = vl(2) - len(a1) = 3 - 3 = 0
- l(2) = vl(4) - len(a2) = 6 - 6 = 0
- l(3) = vl(3) - len(a3) = 3 - 2 = 1
- l(4) = vl(5) - len(a4) = 7 - 4 = 3
- l(5) = vl(4) - len(a5) = 6 - 2 = 4
- l(6) = vl(4) - len(a6) = 6 - 1 = 5
- l(7) = vl(6) - len(a7) = 6 - 3 = 3
- l(8) = vl(5) - len(a8) = 7 - 1 = 6
- l(9) = vl(7) - len(a9) = 10 - 3 = 7
- l(10) = vl(7) - len(a10) = 10 - 4 = 6
| 边 | a1(3) | a2(6) | a3(2) | a4(4) | a5(2) | a6(1) | a7(3) | a8(1) | a9(3) | a10(4) |
|---|---|---|---|---|---|---|---|---|---|---|
| l(i) | 0 | 0 | 1 | 3 | 4 | 5 | 3 | 6 | 7 | 6 |
2.5 求出关键边和关键路径
列出总表:
| 顶点 | ve | vl | 活动 | e | l | l - e | 关键路径 |
|---|---|---|---|---|---|---|---|
| v1 | 0 | 0 | a1 | 0 | 0 | 0 | √ |
| v2 | 3 | 3 | a2 | 0 | 0 | 0 | √ |
| v3 | 2 | 3 | a3 | 0 | 1 | 1 | |
| v4 | 6 | 6 | a4 | 3 | 3 | 0 | √ |
| v5 | 7 | 7 | a5 | 3 | 4 | 1 | |
| v6 | 5 | 6 | a6 | 2 | 5 | 3 | |
| v7 | 10 | 10 | a7 | 2 | 3 | 1 | |
| a8 | 6 | 6 | 0 | √ | |||
| a9 | 7 | 7 | 0 | √ | |||
| a10 | 5 | 6 | 1 |
其中e(i)==l(i)的边:a1 a2 a4 a8 a9
所组成的路径即为关键路径:a1->a4->a9 和 a2->a8->a9
三、代码:
1 |
|
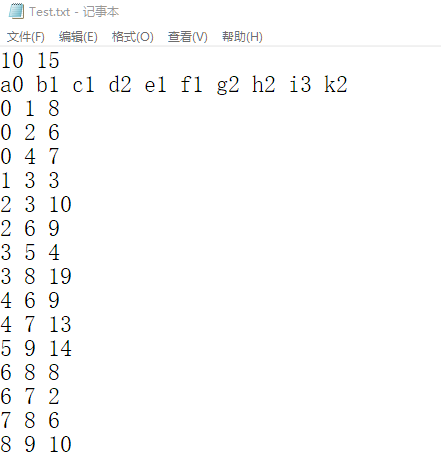
四、文件格式
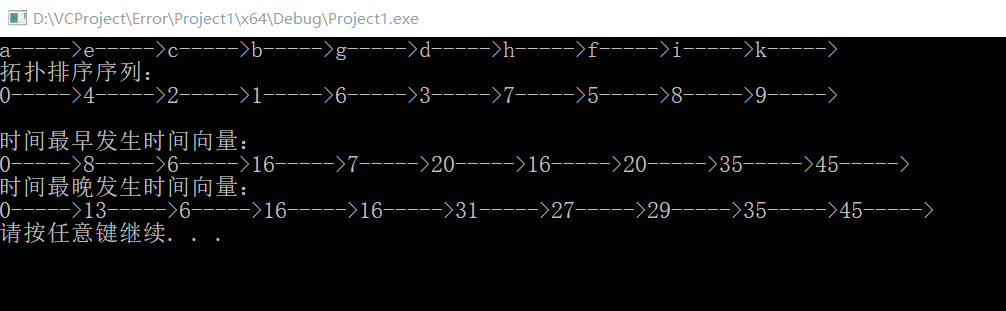
五、输出结果: