机器学习方法(一)：物以类聚人以群分 K近邻算法

2019-07-18

× 文章目录

1. 一、KNN算法概述
1.1. 2.3 特征归一化

2.1. 3.1 简单方法
2.2. 3.2 KD树
2.3. 3.3 构造平衡kd树算法
2.4. 3.4 搜索kd树

一、KNN算法概述

k近邻算法是一种基本分类与回归的方法，在空间中如果一个样本附近的k个最近样本的大多数属于某一个类别，则该样本也属于这个类别。即给定一个训练数据集，对新的输入实例进行归类，类别即为与该实例最近的k个实例中的多数属于的类。k=1时，为最近邻算法。

如下图所示，有两种不同的样本数据，绿色的圆点代表的即为待分类的数据。针对不同的k值，分类结果也会有所不同。

k=3时，绿色圆点的最近的3个邻居是2个红色小三角形和1个蓝色小正方形，少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于红色的三角形一类。 k=5时，绿色圆点的最近的5个邻居是2个红色三角形和3个蓝色的正方形，还是少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于蓝色的正方形一类。 ## 二、三要素 KNN算法需要考虑的三个重要因素：k值的选取、距离度量方式和分类决策规则。 ### 2.1 k值的选取 k值的选择没有一个固定的经验，一般取一个比较小的数值。通常采用**交叉验证法**来选择最优的k值。 ### 2.2 距离度量方式特征空间中两个实例点的距离是两个实例点**相似程度**的反映。特征空间一般是n维实数向量空间$\pmb{R^n}$（欧式空间）。一般的$\pmb{L_p}$距离$(L_p distance)$或闵可夫斯基`(Minkowski)`距离定义：设特征空间 $\chi$ 是 $n$ 维实数向量空间 $\boldsymbol{R}^{n}, x_{i}, x_{j} \in \chi, x_{l}=\left(x_{i}^{(1)}, x_{i}^{(2)}, \ldots, x_{i}^{(n)}\right)^{T}, \quad x_{j}=\left(x_{j}^{(1)}, x_{j}^{(2)}, \ldots, x_{j}^{(n)}\right)^{T}, x_{i}, x_{j}$ 的 $L_{p}$ 距离定义为： $$ L_{p}\left(x_{i}, x_{j}\right)=\left(\sum_{l=1}^{n}\left|x_{i}^{(l)}-x_{j}^{(l)}\right|^{p}\right)^{\frac{1}{p}} $$ + 这里$p≥1$。当$p=2$时，称为**欧氏距离**`（Euclidean distance）`，即： $$ L_{2}\left(x_{i}, x_{j}\right)=\left(\sum_{l=1}^{n}\left|x_{i}^{(l)}-x_{j}^{(l)}\right|^{2}\right)^{\frac{1}{2}} $$ + 当$p=1$时，称为**曼哈顿距离**`（Manhattan distance）`，即： $$ L_{1}\left(x_{i}, x_{j}\right)=\sum_{l=1}^{n}\left|x_{i}^{(l)}-x_{j}^{(l)}\right| $$ #### 2.2.1 欧式距离$(Euclidean\ distance)$

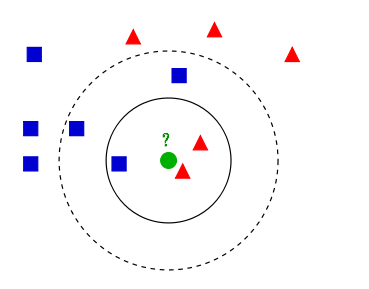
最常见的两点之间或多点之间的距离表示方法，又称为欧几里得度量。

定义于欧几里得空间中，点$x=(x1,…,xn)$和$y=(y1,…,yn)$之间的距离为:

$d(x, y)=\sqrt{\left(x_{1}-y_{1}\right)^{2}+\left(x_{2}-y_{2}\right)^{2}+\cdots+\left(x_{n}-y_{n}\right)^{2}}=\sqrt{\sum_{i=1}^{n}\left(x_{i}-y_{i}\right)^{2}}$

2.2.2 曼哈顿距离($Manhattan distance$)

在欧几里得空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。曼哈顿距离也称为“城市街区距离”(City Block distance)。例如在二维平面上，坐标$(x_1,y_1)$与坐标$(x_2,y_2)$的曼哈顿距离为：$|x_1−x_2|+|y_1−y_2|$。

(1) 二维平面上两点$a(x_1,y_1)$与$b(x_2,y_2)$间的曼哈顿距离：

$d_{12}=|x_1−x_2|+|y_1−y_2|$

(2) 两个$n$维向量$a(x_{11},x_{12},…,x_{1n})$和$b(x_{21},x_{22},…,x_{2n})$间的曼哈顿距离：

$d_{12}=\sum_{k=1}^{n}\left|x_{1 k}-x_{2 k}\right|$

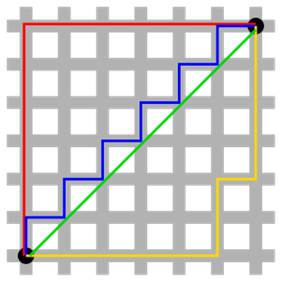
两种距离的对比，如上图所示：红线代表曼哈顿距离，绿色代表欧氏距离，也就是直线距离，而蓝色和黄色分别代表等价的曼哈顿距离。

2.2.3 切比雪夫距离($Chebyshev distance$)

向量空间中的一种度量，二个点之间的距离定义是其各坐标数值差绝对值的最大值。若二个向量或二个点$p、q$，其坐标分别为$p_i、q_i$，则两者之间的切比雪夫距离定义如下：

$D(p, q)=\max \left|p_{i}-q_{i}\right|$

(1) 二维平面两点$a(x_1,y_1)$与$b(x_2,y_2)$间的切比雪夫距离：

$d_{12}=max(|x_1−x_2|,|y_1−y_2|)$

(2) 两个$n$维向量$a(x_{11},x_{12},…,x_{1n})$和$b(x_{21},x_{22},…,x_{2n})$间的切比雪夫距离：

$d_{12}=\max _{i}\left(\left|x_{1 i}-x_{2 i}\right|\right)$

这个公式的另一种等价形式是：

$d_{12}=\lim _{k \rightarrow \infty}\left(\sum_{i=1}^{n}\left|x_{1 i}-x_{2 i}\right|^{k}\right)^{1 / k}$

国际象棋棋盘上，国王走一步能够移动到相邻的8个方格中的任意一个，其中切比雪夫距离指王要从一个位子移至另一个位子至少需要走的步数。你会发现，国王从格子$(x_1,y_1)$走到格子$(x_2,y_2)$最少需要的步数总是$max(|x_2−x_1|,|y_2−y_1|)$步。

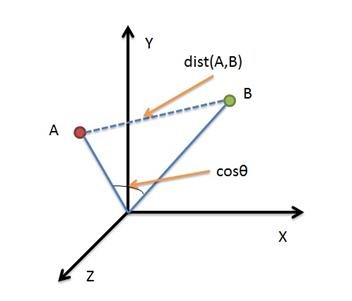
2.2.4 夹角余弦距离

几何中夹角余弦可用来衡量 两个向量方向的差异，在机器学习中特征通常使用向量形式来表示，常用这一概念来衡量样本向量之间的差异。向量方向差异范围：$[−1,1]$

二维空间中的向量$(x_1,y_1)$)与向量$(x_2,y_2)$夹角余弦：

$\cos \theta=\frac{x_{1} x_{2}+y_{1} y_{2}}{\sqrt{x_{1}^{2}+y_{1}^{2}} \sqrt{x_{2}^{2}+y_{2}^{2}}}$

给定两个特征向量$A(x_{11},x_{12},…,x_{1n})$和$B(x_{21},x_{22},…,x_{2n})$，其余弦相似性$\theta$由点积和向量长度给出，如下所示:

$\text { similarity }=\cos (\theta)=\frac{A \cdot B}{\|A\|\|B\|}=\frac{\sum_{i=1}^{n} A_{i} \times B_{i}}{\sqrt{\sum_{i=1}^{n}\left(A_{i}\right)^{2}} \times \sqrt{\sum_{i=1}^{n}\left(B_{i}\right)^{2}}}=\frac{\sum_{i=1}^{n} x_{1 i} x_{2 i}}{\sqrt{\sum_{i=1}^{n} x_{1 i}^{2}} \sqrt{\sum_{i=1}^{n} x_{2 i}^{2}}}$

余弦距离和欧氏距离的区别

从上图可以看出，欧氏距离衡量的是空间各点的绝对距离，跟各个点所在的位置坐标直接相关；而余弦距离衡量的是空间向量的夹角，更加体现在方向上的差异。余弦距离常用于形容两个特征向量之间的关系，例如人脸识别，推荐系统等。

对于向量量$[0,1]$和向量$[1,0]$而言，二者的余弦距很大，而欧氏距离很小；
对于向量$[1,10]$和向量$[10,100]$而言，余弦距离会认为两个特征向量距离很近；但显然这两个特征向量是有着极大差异的，此时我们更关注数值的绝对差异，应当使用欧氏距离。

注：在CNN中，对特征向量进行L2范数归一化后，欧式距离等价于余弦距离。

2.2.5 汉明距离

汉明距离是使用在数据传输差错控制编码里面的，汉明距离是一个概念，它表示两个（相同长度）字对应位不同的数量。也即将其中一个变为另外一个所需要作的最小替换次数。例如1011101 与 1001001 之间的汉明距离是 2。

2.3 特征归一化

数据中不同特征值差距十分大，导致预测结果被某项特征主导，而忽略了其他特征的影响，所以需要进行数据的归一化。

解决方案：将所有数据映射到同一尺度上。

常用的特征归一化方法包括最值归一化和均值方差归一化。

2.3.1 最值归一化($normalization$)

将所有数据映射到0-1之间：

$x_{\text {scale }}=\frac{x-x_{\min }}{x_{\max }-x_{\min }}$

import numpy as np
import matplotlib.pyplot as plt
x = np.random.randint(0,100,100)
# 二维矩阵中分别对每列进行最值归一化
x = np.random.randint(0,100,(50,2))
x = np.array(x,dtype=float)
x[:,0] = (x[:,0] - np.min(x[:,0])) / (np.max(x[:,0]) - np.min(x[:,0]))
x[:,1] = (x[:,1] - np.min(x[:,1])) / (np.max(x[:,1]) - np.min(x[:,1]))
plt.scatter(x[:,0],x[:,1])
plt.show()

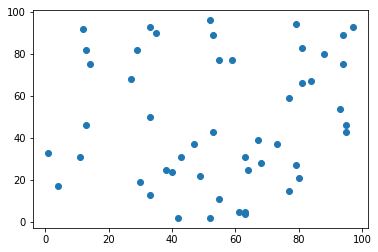
运行结果（左图为归一化前，右图为归一化后）：

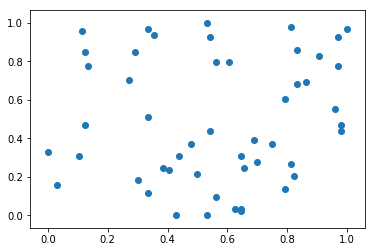
2.3.2 均值方差归一化($standardization$)

将所有数据归一到均值为0方差为1的分布中：

$x_{\text {scale }}=\frac{x-x_{\text {mean }}}{s}$

import numpy as np
import matplotlib.pyplot as plt
# 二维矩阵中分别对每列进行均值方差归一化
x2 = np.random.randint(0,100,(50,2))
x2 = np.array(x2,dtype=float)
x2[:,0] = (x2[:,0] - np.mean(x2[:,0])) / np.std(x2[:,0])
x2[:,1] = (x2[:,1] - np.mean(x2[:,1])) / np.std(x2[:,1])
plt.scatter(x2[:,0],x2[:,1])
plt.show()

运行结果（左图为归一化前，右图为归一化后）：

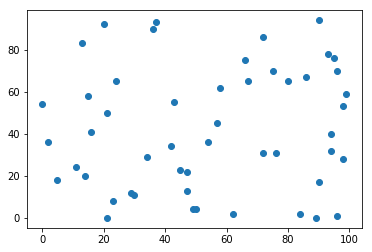
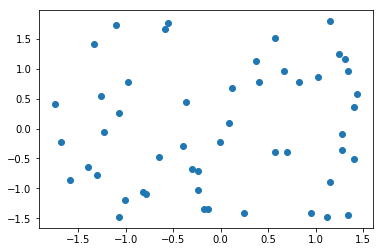
2.3.3 $scikit_learn$中的归一化

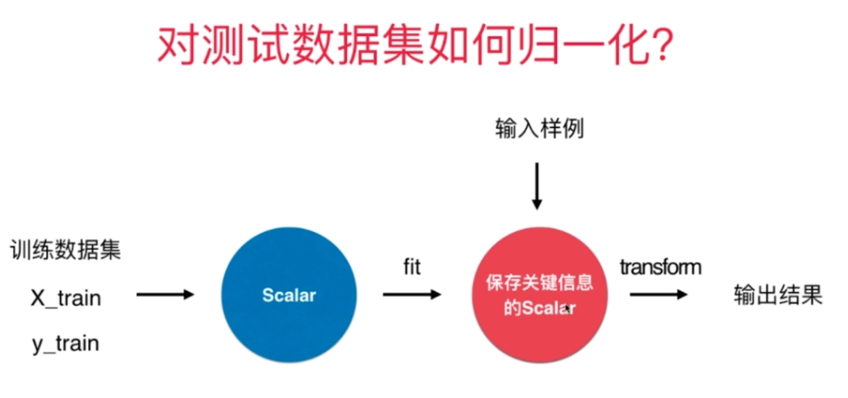
#scikit_learn中的Scalar

import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split


#以鸢尾花的数据集为示例
iris = datasets.load_iris()
X=iris.data
y=iris.target

#创建训练数据集和测试数据集
X_train,x_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=666)

from sklearn.preprocessing import StandardScaler  #sklearn中的相应的类

standardScaler = StandardScaler() #  构造均值方差归一化对象
standardScaler.fit(X_train) # 求出相应的均值和方差（根据训练集）
standardScaler.mean_ # 均值 array([5.83416667, 3.0825    , 3.70916667, 1.16916667])
standardScaler.scale_  # 标准差array([0.81019502, 0.44076874, 1.76295187, 0.75429833])

X_train=standardScaler.transform(X_train)  # 根据fit计算出来的值来进行相应的数据归一化

x_test_transform=standardScaler.transform(x_test)  # 对测试集也使用同样的方法进行相应的数据归一化

from sklearn.neighbors import KNeighborsClassifier  
# 创建一个kNN分类器
knn_clf=KNeighborsClassifier(n_neighbors=3)
knn_clf.fit(X_train,y_train)

'''
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
           metric_params=None, n_jobs=1, n_neighbors=3, p=2,
           weights='uniform')
'''
print(knn_clf.score(x_test,y_test)) # 数据归一化前的精确度
print(knn_clf.score(x_test_transform,y_test)) # 数据归一化后的精确度

运行结果：
1
2
0.3333333333333333
1.0

三、算法实现

3.1 简单方法

按照k邻近的思想，找到kk个最近的邻居来进行预测，就需要计算出预测样本与所有训练集中样本的距离，然后计算出最小的k个距离，接着进行投票表决，即可做出预测。这种思路简单直接，在样本量少、特征少的情况下有效。对于大量的数据而言，特证数和样本量都很大，如果要预测少量的测试集样本，算法的时间效率会很低。

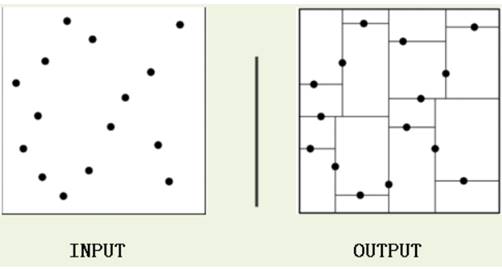
3.2 KD树

kd树(K-dimension tree)是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。kd树是一种二叉树，表示对k维空间的一个划分，构造kd树相当于不断地用垂直于坐标轴的超平面将k维空间切分，构成一系列的k维超矩形区域。利用kd树可以省去对大部分数据点的搜索，从而减少搜索的计算量。

3.3 构造平衡kd树算法

输入：k维空间数据集$T=x_1,x_2,…,x_N$，其中$x_i=(x_i^{(1)},x_i^{(2)},…,x_i^{(k)}),i=1,2,…N$

开始：构造根节点，选择$x^{(1)}$为坐标轴，以$T$中所有实例的$x^(1)$坐标的中位数为切点，将根结点对应的超矩形区域切分为两个子区域。由根节生成深度$1$的左右子节点，左、右子结点分别对应坐标$x^{(1)}$小于、大于切分点的子区域。将落在切分平面上的实例点保存在该结点。
重复：对深度为$\pmb j$的结点，选择x(l)x(l)为切分的坐标轴，$\pmb {l=j \% k+1}$，以该结点的区域中所有实例的$x^{(l)}$坐标的中位数为切分点，将该结点对应的超矩形区域切分为左右两个子区域。将落在切分平面上的实例点保存在该结点。

简单的二维平面的例子：

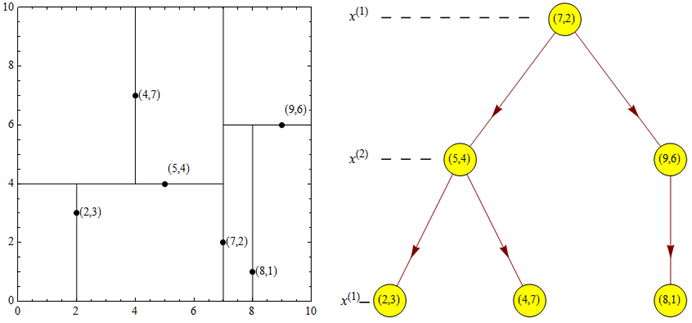
给定一个二维数据集：$T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}$，构造一个平衡kd树。

开始：选择$x^{(1)}$轴， $6$个数据的坐$x^{(1)}$标中位数是$6$，这里选最接近的$(7,2)$点，以平面将$x^{(1)}=7$空间分为左右两个子矩形，并将$(7,2)$点保存在根节点；
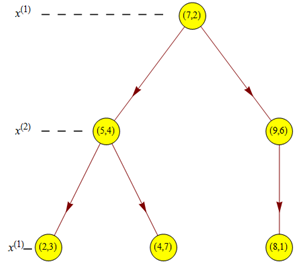
重复：接着计算左矩形中$(2,3),(5,4),(4,7)$点的$x^{(2)}$坐标中位数为$4$，左矩阵以$x^{(2)}=4$分为两个子矩形，并将$(5,4)$点保存在左子节点；再计算右矩形中$(8,1),(9,6)$点的$x^{(2)}$坐标中位数为$6$，左矩阵以$x^{(2)}=6$分为两个子矩形，并将$(9,6)$点保存在右子节点；如此递归，最后得到如下图所示的平衡$kd$树。

3.4 搜索kd树

利用kd树可以省去对大部分数据点的搜索，从而减少搜索的计算量。给定一个目标点，搜索其最近邻，首先找到包含目标点的叶节点；然后从该叶结点出发，依次回退到父结点；不断查找与目标点最近邻的结点，当确定不可能存在更近的结点时终止。

输入：已构造的kd树，目标点$x$;

在kd树中找出包含目标点x的叶结点：从根结点出发，递归的向下访问$kd$树。若目标点当前维的坐标值小于切分点的坐标值，则移动到左子结点，否则移动到右子结点。直到子结点为叶结点为止；
以此叶结点为当前最近点；
递归向上回退，如果该结点保存的实例点比当前最近点距目标点更近，则以该实例点为当前最近点；若当前最近点一定存在于该结点一个子结点对应的区域。检查该子结点的父结点的另一个子结点对应的区域是否有更近的点。
回退到根节点，搜索结束。最后的当前最近点即为x的最近邻点。

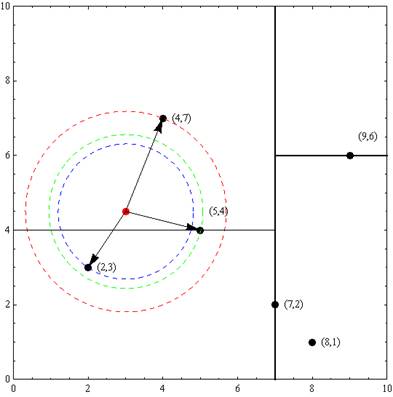
以先前构建好的kd树为例，查找目标点$(3,4.5)$的最近邻点：

首先，通过搜索路径$(7,2)→(5,4)→(4,7)$，找到根节点$(4,7)$取$(4,7)$为当前最近节点。
取$(4,7)$为当前最近邻点。以目标查找点为圆心，目标查找点到当前最近点的距离$2.69$为半径确定一个红色的圆。然后回溯到$(5,4)$，计算其与查找点之间的距离为$2.06$，则该结点比当前最近点距目标点更近，以$(5,4)$为当前最近点。
同样的方法确定一个绿色的圆，该圆$y=4$平面相交，进入$(5,4)$结点的另一个子空间进行查找。结点$(2,3)$与目标点距离为$1.8$，比当前最近点要进，最近邻点更新为$(2,3)$。
根据规则确定蓝色的圆，该圆与$x=7$平面不相交，不用再进入子空间进行查找。
至此，回溯完毕，返回最近邻点$(2,3)$。

代码实现（cs231n）

import numpy as np

class KNearestNeighbor(object):
    """"a kNN classifiers with L2 distance"""

    def __init__(self):
        pass

    def train(self,X,y):
        """
        Train the classifier. For k-nearest neighbors this is just
        memorizing the training data.
        Inputs:
        - X: A numpy array of shape (num_train, D) containing the training data
          consisting of num_train samples each of dimension D.
        - y: A numpy array of shape (N,) containing the training labels, where
             y[i] is the label for X[i].
        """
        self.X_train = X
        self.y_train = y

    def predict(self,X,k=1,num_loops=0):
        """
        :param X: A numpy array of shape (num_test, D) containing test data consisting
             of num_test samples each of dimension D.
        :param k: The number of nearest neighbors that vote for the predicted labels.
        :param num_loops: Determines which implementation to use to compute distances
          between training points and testing points.
        :return: A numpy array of shape (num_test,) containing predicted labels for the
          test data, where y[i] is the predicted label for the test point X[i].
        """

        if num_loops == 0:
            dists = self.compute_distances_no_loops(X)
        elif num_loops == 1:
            dists = self.compute_distances_one_loop(X)
        elif num_loops == 2:
            dists = self.compute_distances_two_loops(X)
        else:
            raise ValueError('Invalid value %d for num_loops' % num_loops)

        return self.predict_labels(dists,k=k)

    def compute_distances_two_loops(self, X):
        """
        Compute the distance between each test point in X and each training point
        in self.X_train using a nested loop over both the training data and the
        test data.
        Inputs:
        - X: A numpy array of shape (num_test, D) containing test data.
        Returns:
        - dists: A numpy array of shape (num_test, num_train) where dists[i, j]
          is the Euclidean distance between the ith test point and the jth training
          point.
        """
        num_test = X.shape[0] # 测试数据行数
        num_train = self.X_train.shape[0] # 训练数据函行数
        dists = np.zeros((num_test,num_train))
        for i in range(num_test):
            for j in range(num_train):
                #####################################################################
                # TODO:                                                             #
                # Compute the l2 distance between the ith test point and the jth    #
                # training point, and store the result in dists[i, j]. You should   #
                # not use a loop over dimension.                                    #
                #####################################################################
                num_test_i = X[i,:]  # num_test的第i行
                num_train_i = self.X_train[j,:]  # num_train的第j行
                 # 求得测试数据的第i行跟第训练数据的第j行差值的平方和
                num_sum = np.sum((num_test_i - num_train_i) ** 2)
                dists[i,j] = np.sqrt(num_sum)  # 开平方根求距离
                #####################################################################
                #                       END OF YOUR CODE                            #
                #####################################################################
        return dists

    def compute_distances_one_loop(self, X):
        """
        Compute the distance between each test point in X and each training point
        in self.X_train using a single loop over the test data.
        Input / Output: Same as compute_distances_two_loops
        """

        num_test = X.shape[0]
        num_train = self.X_train.shape[0]
        dists = np.zeros((num_test,num_train))
        for i in range(num_test):
            #######################################################################
            # TODO:                                                               #
            # Compute the l2 distance between the ith test point and all training #
            # points, and store the result in dists[i, :].                        #
            #######################################################################
            num_test_i = X[i,:]  # 测试数据的第i行
            num_row = np.sum((num_test_i - self.X_train) ** 2,axis=1)  # 返回每行的计算平方和的结果
            dists[i,:] = np.sqrt(num_row)  # 直接赋值第i行
            #######################################################################
            #                         END OF YOUR CODE                            #
            #######################################################################
        return dists

    def compute_distances_no_loops(self, X):
        """
        Compute the distance between each test point in X and each training point
        in self.X_train using no explicit loops.
        Input / Output: Same as compute_distances_two_loops
        """
        num_test = X.shape[0]  # 第一维的大小
        num_train = self.X_train.shape[0]  # 训练数据的第一维大小
        dists = np.zeros((num_test,num_train))
        #########################################################################
        # TODO:                                                                 #
        # Compute the l2 distance between all test points and all training      #
        # points without using any explicit loops, and store the result in      #
        # dists.                                                                #
        #                                                                       #
        # You should implement this function using only basic array operations; #
        # in particular you should not use functions from scipy.                #
        #                                                                       #
        # HINT: Try to formulate the l2 distance using matrix multiplication    #
        #       and two broadcast sums.                                         #
        #########################################################################
        X_sum = np.sum(np.power(X,2),axis=1)  # 每一行平方和
        X_C_1 = np.reshape(X_sum,(-1,1))  # 行向量转为列向量
        X_C_2 = -2 * np.dot(X,self.X_train.T)  # -2倍的A·𝐵𝑇
        X_C_3 = np.sum(np.power(self.X_train,2),axis=1)
        dists = np.sqrt(X_C_1 + X_C_2 + X_C_3)
        #########################################################################
        #                         END OF YOUR CODE                              #
        #########################################################################
        return dists

    def predict_labels(self, dists, k=1):
        """
        Given a matrix of distances between test points and training points,
        predict a label for each test point.
        Inputs:
        - dists: A numpy array of shape (num_test, num_train) where dists[i, j]
          gives the distance betwen the ith test point and the jth training point.
        Returns:
        - y: A numpy array of shape (num_test,) containing predicted labels for the
          test data, where y[i] is the predicted label for the test point X[i].
        """
        num_test = dists.shape[0]
        y_pred = np.zeros(num_test)
        for i in range(num_test):
            # A list of length k storing the labels of the k nearest neighbors to
            # the ith test point.
            closest_y = []
            #########################################################################
            # TODO:                                                                 #
            # Use the distance matrix to find the k nearest neighbors of the ith    #
            # testing point, and use self.y_train to find the labels of these       #
            # neighbors. Store these labels in closest_y.                           #
            # Hint: Look up the function numpy.argsort.                             #
            #########################################################################
            nearrest = np.argsort(dists[i,:])  # 返回每一行排序后的结果索引
            closest_y = [self.y_train[i] for i in nearrest[:k]]  # 距离最近的前k个元素的y_train值
            #########################################################################
            # TODO:                                                                 #
            # Now that you have found the labels of the k nearest neighbors, you    #
            # need to find the most common label in the list closest_y of labels.   #
            # Store this label in y_pred[i]. Break ties by choosing the smaller     #
            # label.                                                                #
            #########################################################################
            dict = {}
            for key in closest_y:  # 遍历计算每个key出现的次数
                if key in dict:
                    dict[key] += 1
                else:
                    dict[key] = 1
            # for key in closest_y:  # 遍历计算每个key出现的次数
            #     dict[key] = dict.get(key,0) + 1
            common_label,common_value = max(dict.items(),key=lambda item:item[1])  # 找出出现次数最多的label
            y_pred[i] = common_label
            #########################################################################
            #                           END OF YOUR CODE                            #
            #########################################################################
        return y_pred

四、KNN算法的缺陷

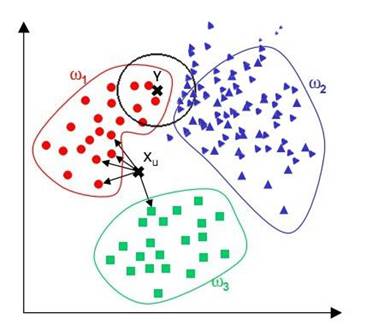
观察上图，可以看到对于样本$X_u$，通过knn算法，显然可以得到$X_u$应属于$w_1$，但对于样本$Y$，通过 knn算法最终似乎得到了$Y$应属于$w_2$的结论，而这个结论直观来看并没有说服力。
当样本不平衡时，knn似乎只关心哪类样本的数量最多，而不去把距离远近考虑在内
改进：可以采用权值的方法来改进。和该样本距离小的邻居权值大，和该样本距离大的邻居权值则相对较小，以此来避免因一个样本过大导致误判**的情况。

HowardWang