机器学习方法(二)：线性回归

2019-07-28

× 文章目录

1. 线性回归
2. Reference

线性回归

线性回归是在假设特征满足线性关系，根据给定的训练数据训练一个线性模型，并用此模型进行预测。即使用一条函数曲线使其训练数据很好的拟合已知函数，并很好的预测未知数据。回归问题按照输入变量的个数可以分为一元回归和多元回归。

一、单变量线性回归

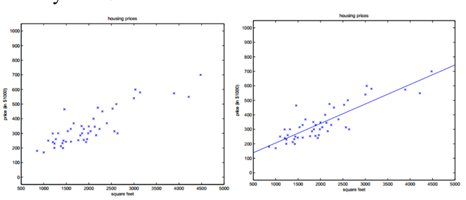
对于一元线性回归，函数用可以用一个公式来表示，即假设 $x$ 和 $h_{\theta}(x)$ 之间存在这样的关系：

\begin{matrix} h_{θ} (x) = θ_{0} + θ_{1} x \\ (1) \end{matrix}

$\begin{equation} h_{\theta}(x) = \theta_0 + \theta_1 x \tag{1} \end{equation}$

$h_{\theta}(x)$ 即我们预测的数值，该值与实际数值之间的差异，即为误差：

\begin{matrix} e r r o r = | y - h_{θ} (x) | \\ (2) \end{matrix}

$\begin{equation} error=|y- h_{\theta}(x)| \tag{2} \end{equation}$

由于求绝对值过于繁琐，我们将其视为误差平方和，并对齐求均值，即代价（损失）函数：

\begin{matrix} J (θ_{0}, θ_{1}) = \frac{1}{2 m} m \sum i = 1 {(h_{θ} (x^{(i)}) - y^{(i)})}^{2} = \frac{1}{2 m} m \sum i = 1 {(θ_{0} + θ_{1} x_{i} - y^{(i)})}^{2} \\ (3) \end{matrix}

$\begin{equation} J\left(\theta_0,\theta_1\right) = \frac{1}{2m}\sum_{i=1}^{m}\left(h_{\theta}(x^{(i)}) - y^{(i)}\right)^{2}=\frac{1}{2m}\sum_{i=1}^{m}\left(\theta_0 + \theta_1x_i-y^{(i)}\right)^{2} \tag{3} \end{equation}$

我们的目的就是使得预测值尽可能地接近实际值，即误差越小越好。即找到一组 $(\theta_0,\theta_1)$ ，使得误差平方和最小。

Hypothesis： $h_{\theta}(x) = \theta_0 + \theta_1 x$

Parameters： $\theta_0,\theta_1$

Cost Function： $J(\theta_0,\theta_1) = \frac{1}{2m}\sum_{i=1}^{m}\left(h_{\theta}(x^{(i)}) - y^{(i)}\right)^{2}$

Goal： $\underset{\theta_{0}, \theta_{1}}{\operatorname{minimize}} J\left(\theta_{0}, \theta_{1}\right)$

二、多元线性回归

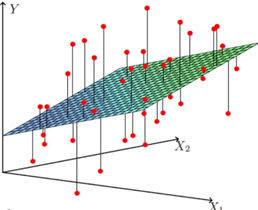
对于多元线性回归而言：

\begin{matrix} \begin{matrix} h_{θ} (x) & = θ_{0} + θ_{1} x_{1} + θ_{2} x_{2} + \dots + θ_{n} x_{n} = n \sum i = 0 θ_{i} x_{i} = θ^{T} x \end{matrix} \\ (4) \end{matrix}

$\begin{equation} \begin{aligned} h_{\theta}(x) &=\theta_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}+\cdots+\theta_{n} x_{n} \\ &=\sum_{i=0}^{n} \theta_{i} x_{i}=\theta^{T} x \end{aligned} \tag{4} \end{equation}$

使用极大似然函数来解释最小二乘：

\begin{matrix} y^{(i)} = θ^{T} X^{(i)} + ε^{(i)} \\ (5) \end{matrix}

$\begin{equation} y^{(i)}=\theta^{T} X^{(i)}+\varepsilon^{(i)} \tag{5} \end{equation}$

根据中心极限定理，误差 $\varepsilon^{(i)}(1≤i≤n)$ 是独立同分布的，服从均值为0，方差为特定 $\sigma^2$ 的高斯分布。

\begin{matrix} P (ε^{(i)}) = \frac{1}{\sqrt{2 π} σ} exp ⎛ ⎝ - \frac{{(ε^{(i)})}^{2}}{2 σ^{2}} ⎞ ⎠ \\ (6) \end{matrix}

$\begin{equation} P(\varepsilon^{(i)})=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(\varepsilon^{(i)}\right)^{2}}{2 \sigma^{2}}\right) \tag{6} \end{equation}$

将式 $(5)$ 带入式 $(6)$ 中可得：

\begin{matrix} P (y^{(i)} | x^{(i)}; θ) = \frac{1}{\sqrt{2 π} σ} exp ⎛ ⎝ - \frac{{(y^{(i)} - θ^{T} X^{(i)})}^{2}}{2 σ^{2}} ⎞ ⎠ \\ (7) \end{matrix}

$\begin{equation} P\left(y^{(i)}|x^{(i)};\theta\right)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y^{(i)}-\theta^TX^{(i)}\right)^{2}}{2 \sigma^{2}}\right) \tag{7} \end{equation}$

其似然函数：

\begin{matrix} L (θ) & = m \prod i = 1 P (y^{(i)} ∣ x^{(i)}; θ) = m \prod i = 1 \frac{1}{\sqrt{2 π} σ} exp ⎛ ⎝ \frac{{- (y^{(i)} - θ^{T} x^{(i)})}^{2}}{2 σ^{2}} ⎞ ⎠ \end{matrix}

$\begin{aligned} L(\theta) &=\prod_{i=1}^{m} P\left(y^{(i)} \mid x^{(i)} ; \theta\right) \\ &=\prod_{i=1}^{m} \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(\frac{\left.-( y^{(i)}-\theta^{T} x^{(i)}\right)^{2}}{2 \sigma^{2}}\right) \end{aligned}$

高斯的对数似然与最小二乘

\begin{matrix} l (θ) & = l o g L (θ) = l o g ⎛ ⎝ m \prod i = 1 \frac{1}{\sqrt{2 π} σ} exp ⎛ ⎝ \frac{{- (y^{(i)} - θ^{T} x^{(i)})}^{2}}{2 σ^{2}} ⎞ ⎠ ⎞ ⎠ = m \sum i = 1 l o g ⎛ ⎝ \frac{1}{\sqrt{2 π} σ} exp ⎛ ⎝ \frac{{- (y^{(i)} - θ^{T} x^{(i)})}^{2}}{2 σ^{2}} ⎞ ⎠ ⎞ ⎠ = m \cdot l o g \frac{1}{\sqrt{2 π} σ} - \frac{1}{σ^{2}} \cdot \frac{1}{2} m \sum i = 1 {(y^{(i)} - θ^{T} X^{(i)})}^{2} \end{matrix}

$\begin{aligned} l(\theta) &= logL(\theta) \\ &= log\left(\prod_{i=1}^{m} \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(\frac{\left.-( y^{(i)}-\theta^{T} x^{(i)}\right)^{2}}{2 \sigma^{2}}\right)\right) \\ &= \sum_{i=1}^{m} log\left(\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(\frac{\left.-( y^{(i)}-\theta^{T} x^{(i)}\right)^{2}}{2 \sigma^{2}}\right)\right) \\ &= m\cdot log\frac{1}{\sqrt{2\pi}\sigma} - \frac{1}{\sigma^2} \cdot \frac{1}{2} \sum_{i=1}^{m}\left(y^{(i)} - \theta^TX^{(i)} \right)^2 \\ \end{aligned}$

其中 $m\cdot log\frac{1}{\sqrt{2\pi}\sigma}$ 为常数，则关于θ的代价函数为：

J (θ) = \frac{1}{2} m \sum i = 1 {(h_{θ} (X^{(i)}) - y^{(i)})}^{2}

$J(\theta)=\frac{1}{2} \sum_{i=1}^{m}\left(h_{\theta}\left(X^{(i)}\right)-y^{(i)}\right)^{2}$

1 2	temp=(X * theta - y)' * (X * theta - y); J=1 / (2 * m) * temp;

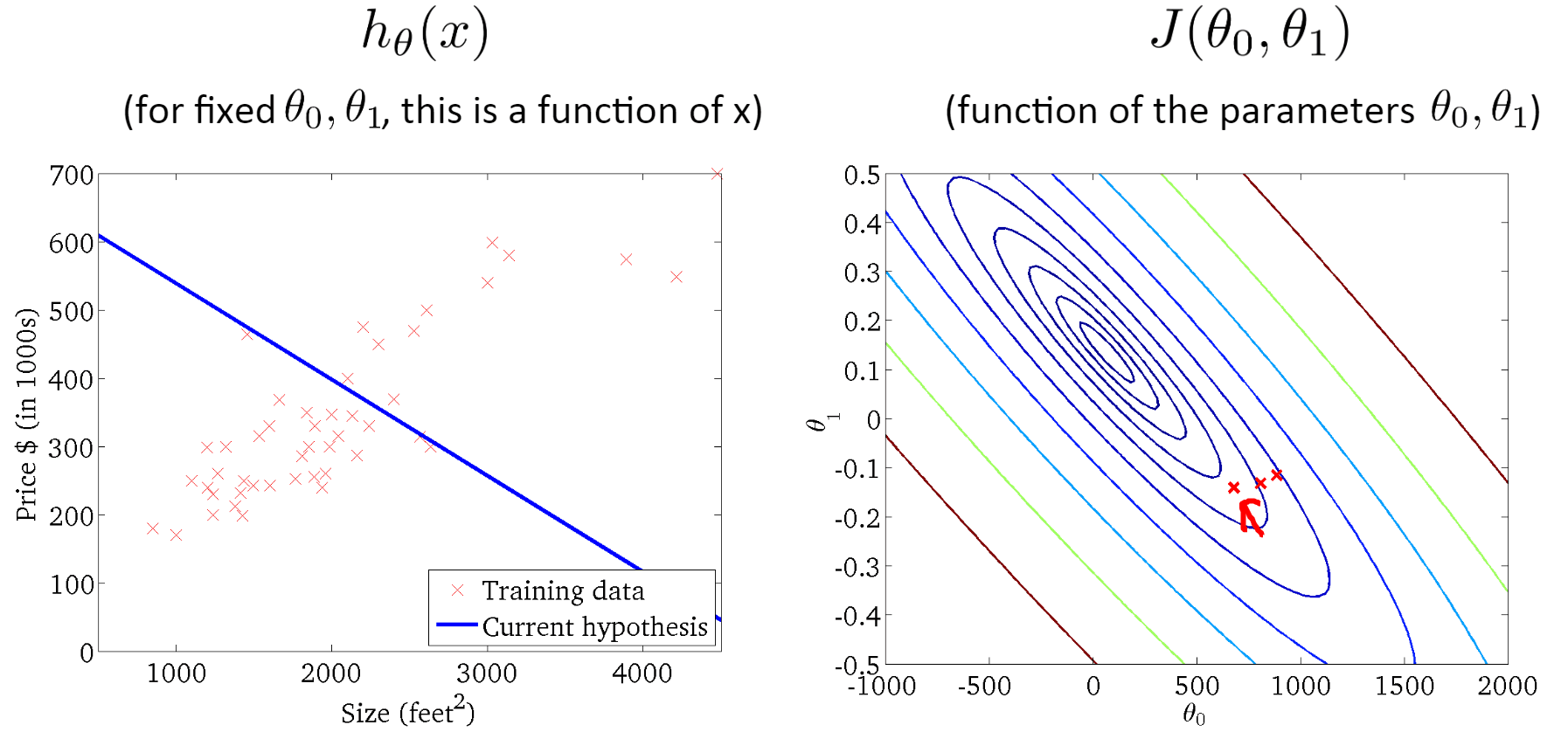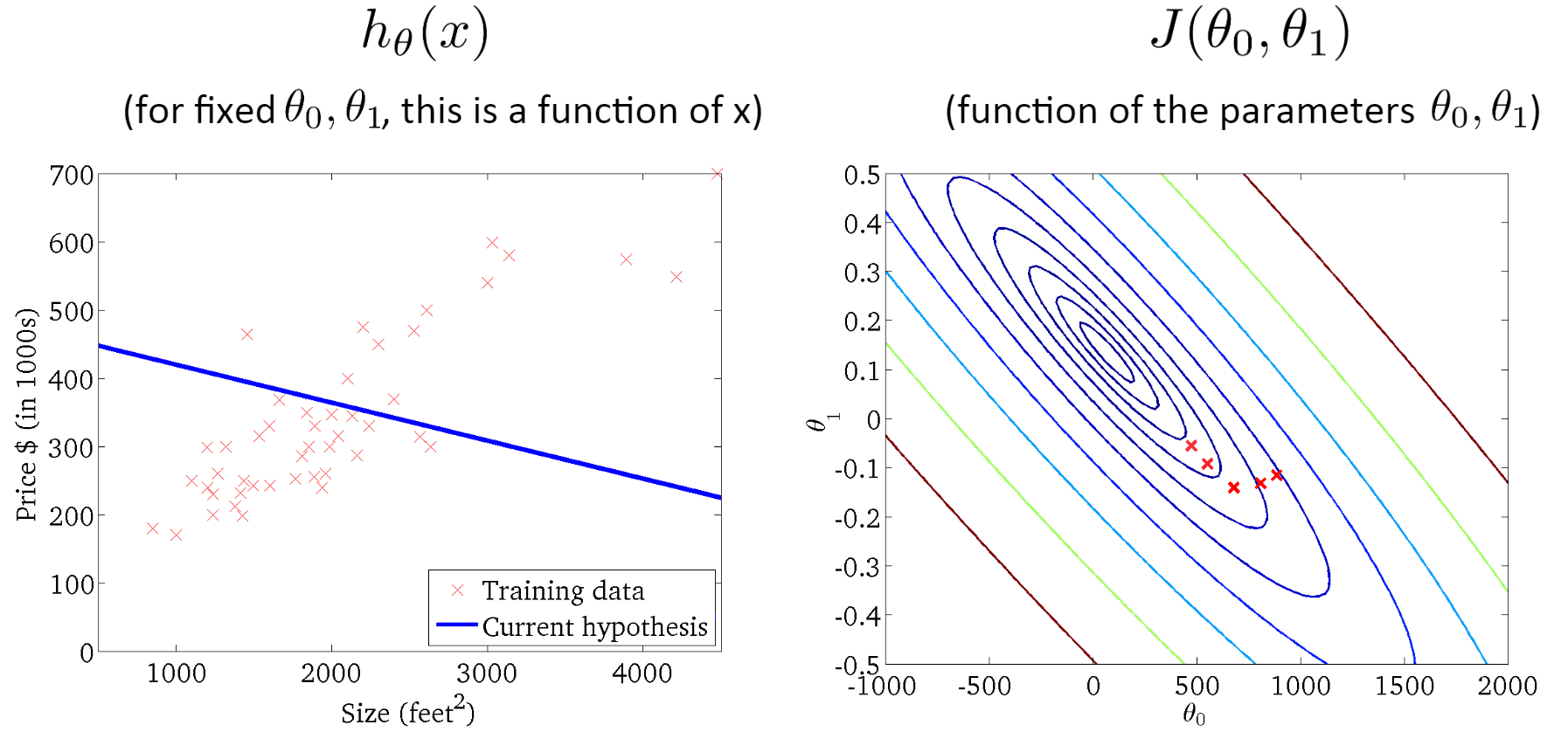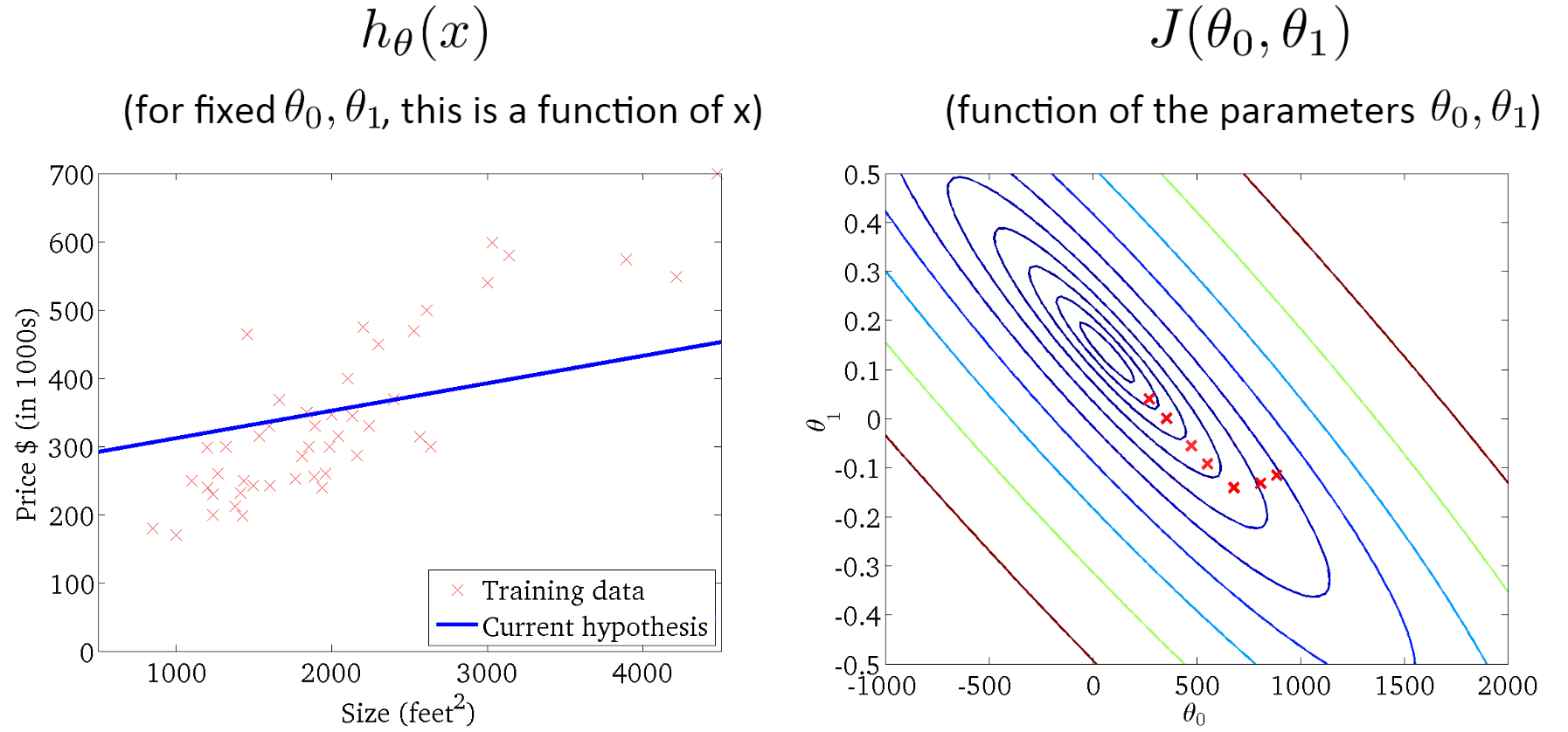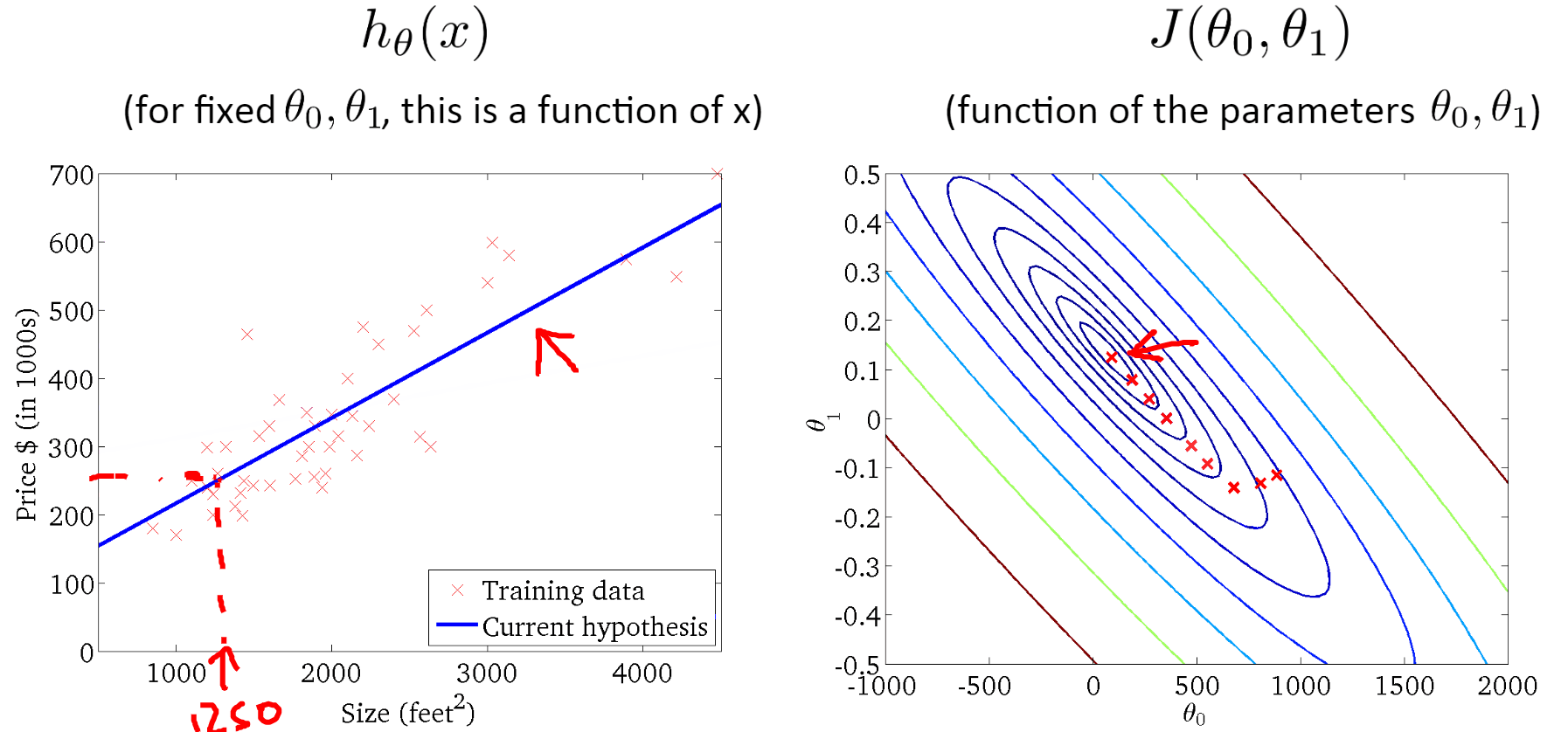
三、梯度下降算法

可以理解为一个人下山的过程，如果想要快速走下山，但是又不知道方向，怎么办呢？显然很容易想到的是一定往下山的方向走。但是选哪个方向呢？这就需要有冒险精神，每次选择最陡峭的方向，即山高度下降最快的地方，这样下山最快。

但是，又有一个问题来了，没有办法每次选择的都是最陡峭的地方。这就需要每次都选定一段距离，每走一段距离之后，就重新确定当前所在位置的高度下降最快的地方。这样，这个人每次下山的方向都可以近似看作是每个距离段内高度下降最快的地方。

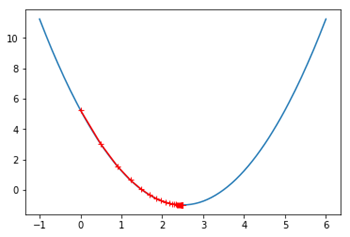
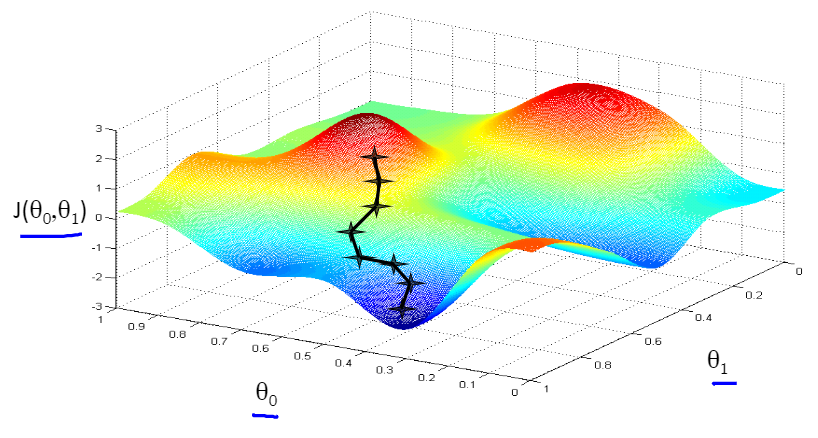
将下山的例子中每一段路的距离取名叫学习率（Learning Rate，也称步长，用α表示），把一次下山走一段距离叫做一次迭代。算法详细过程：

确定定参数的初始值，计算损失函数的偏导数。
将参数代入偏导数计算出梯度。若梯度为 0，结束；否则转到 3。
用步长乘以梯度，并对参数进行更新。

重复2-3，对于多元线性回归来说，拟合函数为：

h_{θ} (x) = n \sum i = 0 θ_{i} x_{i} = θ_{0} + θ_{1} x + \dots + θ_{n} x_{n}

$h_{\theta}(x)=\sum_{i=0}^{n} \theta_{i} x_{i}=\theta_{0}+\theta_{1} x+\cdots+\theta_{n} x_{n}$

损失函数为：

J (θ) = \frac{1}{2 m} n \sum i = 0 {(y^{(i)} - h_{θ} (x^{(i)}))}^{2}

$J(\theta)=\frac{1}{2 m} \sum_{i=0}^{n}\left(y^{(i)}-h_{\theta}\left(x^{(i)}\right)\right)^{2}$

损失函数的偏导数为：

\frac{\partial J (θ)}{\partial θ_{i}} = \frac{1}{m} m \sum j = 1 (h_{θ} (x^{(j)}) - y^{(j)}) x_{i}^{(j)} = \frac{1}{m} m \sum j = 1 (n \sum i = 0 θ_{i} x_{i}^{(j)} - y^{(j)}) x_{i}^{(j)}, (i = 0, 1, 2, 3, \dots, n)

$\frac{\partial J(\theta)}{\partial \theta_{i}}=\frac{1}{m} \sum_{j=1}^{m}\left(h_{\theta}\left(x^{(j)}\right)-y^{(j)}\right) x_{i}^{(j)}=\frac{1}{m} \sum_{j=1}^{m}\left(\sum_{i=0}^{n} \theta_{i} x_{i}^{(j)}-y^{(j)}\right) x_{i}^{(j)},(i=0,1,2,3, \ldots, n)$

每次更新参数的操作为：

θ_{i} = θ_{i} - α \frac{\partial J (θ)}{θ_{i}} = θ_{i} - α \frac{1}{m} m \sum j = 1 (h_{θ} (x^{(j)}) - y^{(j)}) x_{i}^{(j)}

$\theta_{i}=\theta_{i}-\alpha \frac{\partial J(\theta)}{\theta_{i}}=\theta_{i}-\alpha \frac{1}{m} \sum_{j=1}^{m}\left(h_{\theta}\left(x^{(j)}\right)-y^{(j)}\right) x_{i}^{(j)}$

for iter = 1:num_iters
    h = X * theta;
    temp(:,iter) = theta - ((alpha / m) * (X' * (h - y)));
    theta = temp(:,iter);

四、正规方程（最小二乘）

得到多元线性回归的代价函数，可以通过求导和梯度下降来寻找最优的参数。

一元线性回归是对a、b求偏导，多元线性回归是对θ求偏导，即：

目标函数

J (θ) = \frac{1}{2 m} m \sum i = 1 {(h_{θ} (X^{(i)}) - y^{(i)})}^{2} = \frac{1}{2 m} (X θ - y)^{T} \cdot (X θ - y)

$J(\theta)=\frac{1}{2m} \sum_{i=1}^{m}\left(h_{\theta}\left(X^{(i)}\right)-y^{(i)}\right)^{2}=\frac{1}{2m}(X\theta-y)^T \cdot (X\theta - y)$

对 $\theta$ 求梯度：

\begin{matrix} \nabla_{θ} J (θ) & = \nabla_{θ} (\frac{1}{2 m} (X θ - y)^{T} \cdot (X θ - y)) = \frac{1}{2 m} \nabla_{θ} ((θ^{T} X^{T} - y^{T}) \cdot (X θ - y)) = \frac{1}{2 m} \nabla_{θ} (θ^{T} X^{T} X θ - θ^{T} X^{T} y - y^{T} X θ + y^{T} y) = \frac{1}{2 m} (\frac{\partial (θ^{T} X^{T} X θ)}{\partial θ} - \frac{\partial (θ^{T} X^{T} y)}{\partial θ} - \frac{\partial (y^{T} X θ)}{\partial θ} + \frac{\partial (y^{T} y)}{\partial θ}) \end{matrix}

$\begin{aligned} \nabla_{\theta}J(\theta) &= \nabla_{\theta}\left(\frac{1}{2m}(X\theta-y)^T \cdot (X\theta - y)\right) \\ &= \frac{1}{2m} \nabla_{\theta}\left(\left(\theta^TX^T-y^T\right) \cdot (X\theta - y)\right) \\ &= \frac{1}{2m} \nabla_{\theta}\left(\theta^TX^TX\theta - \theta^TX^Ty - y^TX\theta + y^Ty\right) \\ &= \frac{1}{2m} \left(\frac{\partial(\theta^TX^TX\theta)}{\partial \theta} - \frac{\partial(\theta^TX^Ty)}{\partial \theta} - \frac{\partial(y^TX\theta)}{\partial \theta} + \frac{\partial(y^Ty)}{\partial \theta} \right) \end{aligned}$

矩阵（向量）求导法则

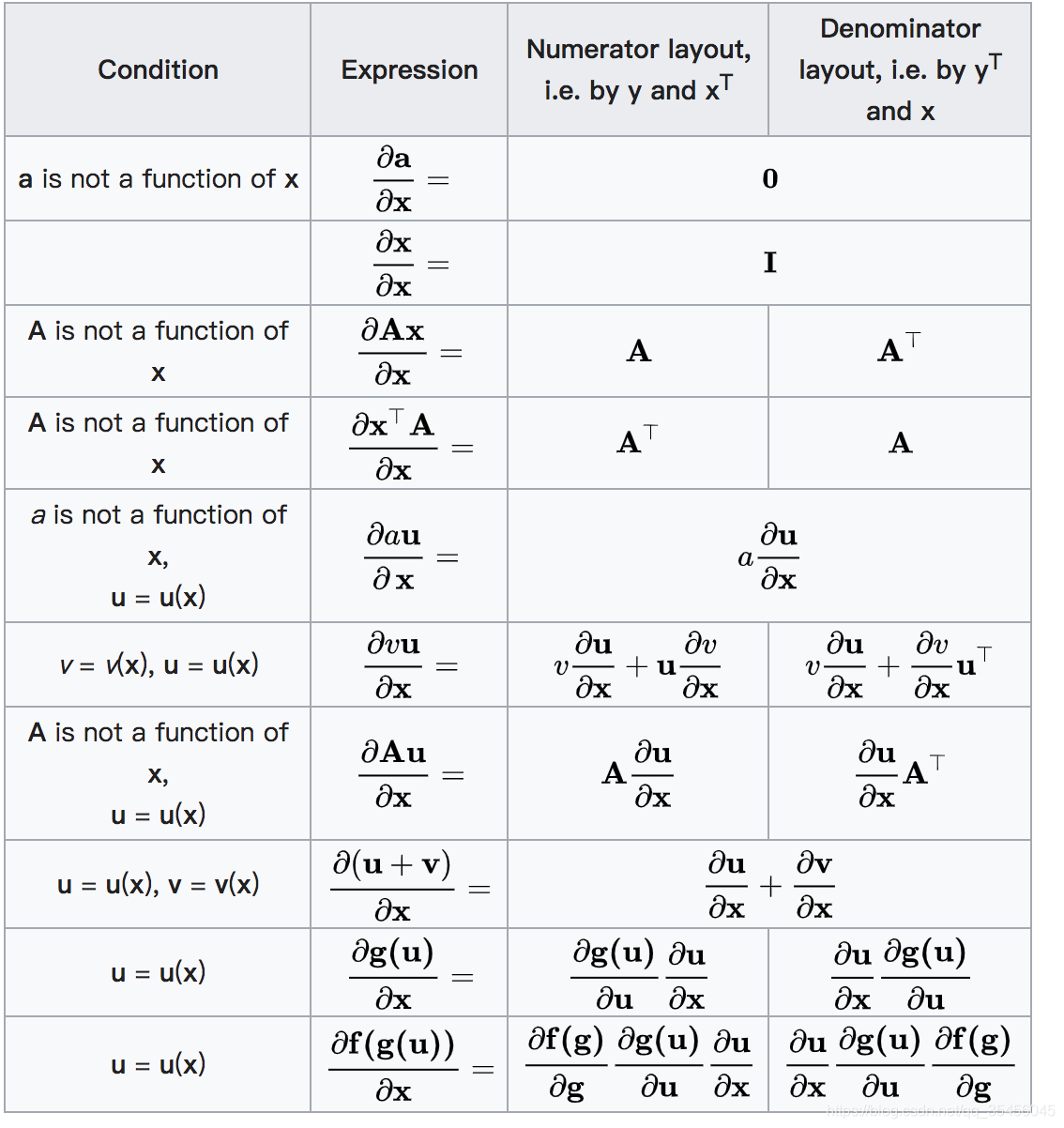
其中第一项： $\frac{\partial}{\partial \theta} \theta^TX^TX\theta$ ，由矩阵求导法则：

\frac{\partial θ^{T} A θ}{\partial θ} = (A + A^{T}) θ （ A 是 不 含 有 X 中 包 含 项 的 矩 阵 ）

$\frac{\partial \theta^T A \theta}{\partial \theta} = (A + A^T) \theta （A是不含有X中包含项的矩阵）$

将 $X^TX$ 看作 $A$ ，可得：

\frac{\partial θ^{T} X^{T} X θ}{\partial θ} = (X^{T} X + X^{T} X) θ = 2 X^{T} X θ

$\frac{\partial \theta^T X^T X \theta}{\partial \theta} = (X^TX + X^TX)\theta = 2X^TX\theta$

第二项： $\frac{\partial}{\partial \theta} \theta^TX^Ty$

矩阵求导法则：
$\frac{\partial X^TA}{\partial X} = A$

将 $X^Ty$ 看作 $A$ ，可得：

\frac{\partial (θ^{T} X^{T} y)}{\partial θ} = X^{T} y

$\frac{\partial(\theta^TX^Ty)}{\partial \theta} = X^Ty$

第三项： $\frac{\partial}{\partial \theta} y^TX\theta$

矩阵求导法则：
$\frac{\partial AX}{\partial X} = A^T$

将 $y^TX$ 看作 $A$ ，可得：

\frac{\partial (y^{T} X θ)}{\partial θ} = X^{T} y

$\frac{\partial(y^TX\theta)}{\partial \theta} = X^Ty$

第四项： $\frac{\partial}{\partial \theta} y^Ty$

矩阵求导法则：
$\frac{\partial A}{\partial X} = 0$

将 $y^Ty$ 看作 $A$ ，可得：

\frac{\partial (y^{T} y)}{\partial θ} = 0

$\frac{\partial(y^Ty)}{\partial \theta} = 0$

综上所述

\begin{matrix} \nabla_{θ} J (θ) & = \frac{1}{2 m} (\frac{\partial (θ^{T} X^{T} X θ)}{\partial θ} - \frac{\partial (θ^{T} X^{T} y)}{\partial θ} - \frac{\partial (y^{T} X θ)}{\partial θ} + \frac{\partial (y^{T} y)}{\partial θ}) = \frac{1}{2 m} (2 X^{T} X θ - 2 X^{T} y) = \frac{1}{m} (X^{T} X θ - X^{T} y) \end{matrix}

$\begin{aligned} \nabla_{\theta}J(\theta) &= \frac{1}{2m} \left(\frac{\partial(\theta^TX^TX\theta)}{\partial \theta} - \frac{\partial(\theta^TX^Ty)}{\partial \theta} - \frac{\partial(y^TX\theta)}{\partial \theta} + \frac{\partial(y^Ty)}{\partial \theta} \right) \\ & = \frac{1}{2m} \left(2X^TX\theta - 2X^Ty\right) \\ & = \frac{1}{m} \left(X^TX\theta - X^Ty\right) \end{aligned}$

当 $\nabla_{\theta}J(\theta) = 0$ 时

X^{T} X θ = X^{T} y θ = (X^{T} X)^{- 1} X^{T} y

$X^TX\theta = X^Ty \\ \theta = (X^TX)^{-1}X^Ty$

如果 $X^TX$ 不可逆，可能有两个原因：

列向量线性相关，即训练集中存在冗余特征，此时应该剔除掉多余特征；
特征过多，此时应该去掉影响较小的特征，或使用“正则化”；

方法选择

	梯度下降法	正规方程法
学习率 $\alpha$	需要	不需要
特征归一化	需要	不需要
计算次数	需要迭代很多次	不需要迭代
特征数量	受特征数量影响较小，即使 $n$ 很大也可以正常工作	如果 $n$ 很大计算速度会很慢

线性回归

一、 单变量线性回归

二、多元线性回归

三、梯度下降算法

四、正规方程（最小二乘 ）

Reference

一、单变量线性回归

四、正规方程（最小二乘）