广义线性模型
对于线性回归而言,模型可以简写为:
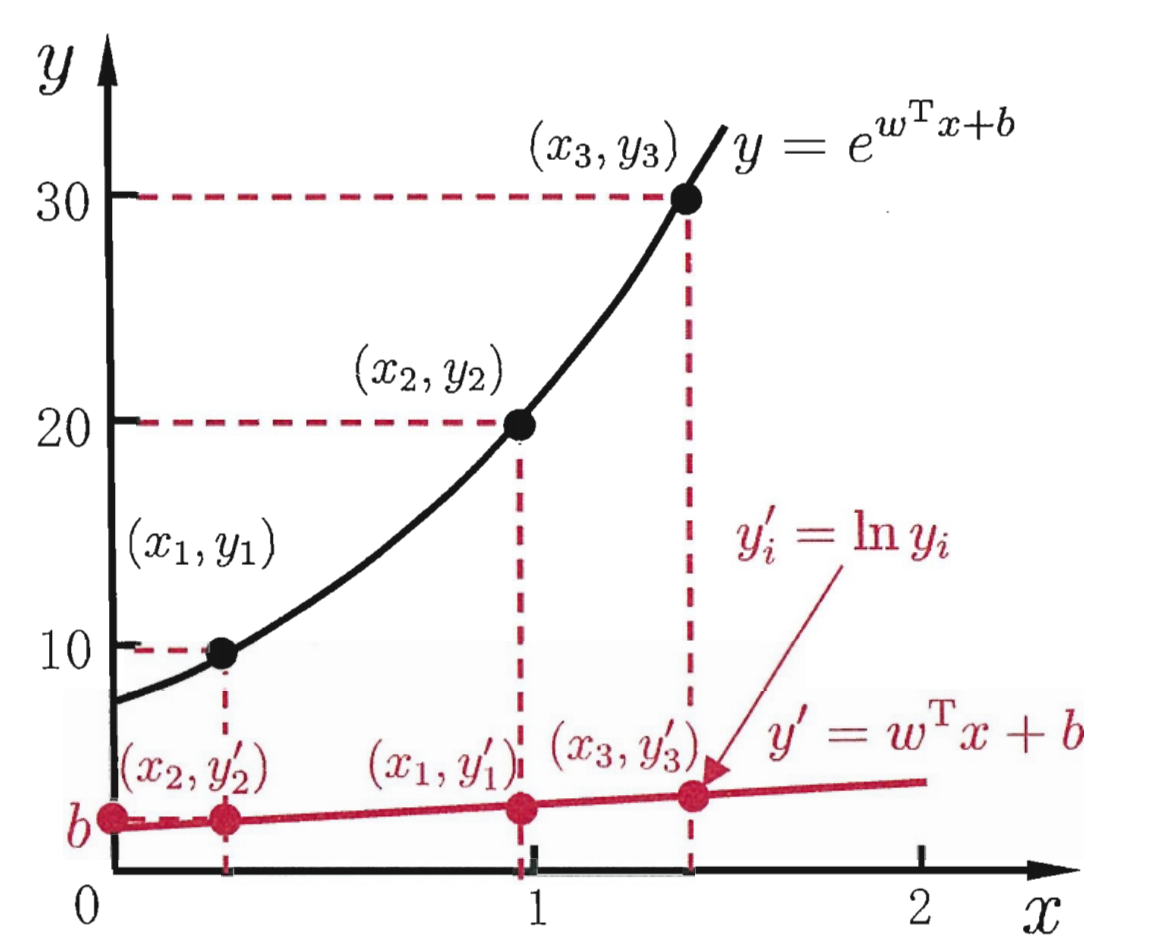
假设我们的模型的输出是在指数尺度上的变化,我们可以简单的将输出的对数作为线性模型逼近的目标,将线性模型映射到指数变化上,即:
这就是“对数线性回归”(log-linear regression),如上图中的红线映射到黑色的指数线,这就是广义线性模型的思想。更一般的考虑单调可微函数g(·),令:
这就得到了“广义线性模型”,虽然在形式上还是线性回归,但实质上是对输入空间的非线性变化,使得函数具有非线性的属性。
一、对数几率回归
虽然被称为“回归”,但是对数几率回归(Logistic Regression)不是用来解决回归问题的,而是用来解决分类问题的。对于简单的二分类问题,实际上是样本点到一个值域y∈{0,1}y∈{0,1}的函数,表示这个点分在正类(postive)或者反类(negtive)的概率,若该样本非常可能是正类,那么输出的概率值越接近1;反之,若该样本非常可能是负类,则输出的概率值越接近0。
而线性回归模型产生的预测值$y=wT+b$是实数值,于是需要一个理想的函数来实现输出实数值z到0/1值的转化。最理想的是单位阶跃函数(uint-step function):
而线性回归模型产生的预测值y=wT+by=wT+b是实数值,于是需要一个理想的函数来实现输出实数值zz到0/10/1值的转化。最理想的是单位阶跃函数(uint-step function):
然而该函数不连续,于是我们希望能够找到一个近似单位越界函数,并且单调可微的函数来代替。
对数几率函数(sigmoid function)正是一个常用的替代函数:
它将z的值转化为一个接近0或1的y值,将对数几率函数作为式$(3)$中的$g(·)$,可得:
二者的图像如下图所示:
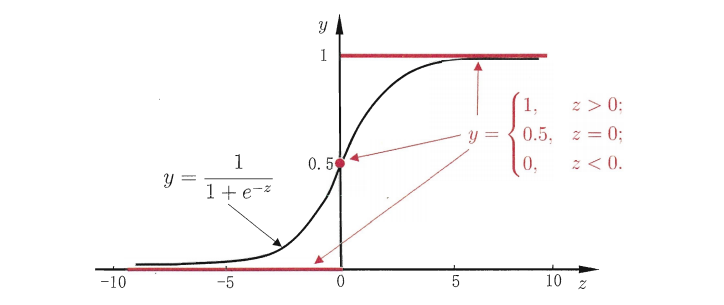
从上图可以看出,它将$z$值转换为一个接近$0$或$1$的$y$值,我们可以将其视为类$1$的后验概率估计$hθ=P(y=1|x;θ)hθ=P(y=1|x;θ)$,即输入一个测试数据$x$,通过$Sigmoid$函数计算出来的结果即为该点$x$输入类别$1$的概率大小。
通常我们将$g(z)≥0.5$ 的归为类别$1$,即预测结果$y=1$;$g(z)<0.5$ 的归为类$0$, 即预测结果$y=0$:
对于式 $(1),$ 式 $(6),$ 可变换为 $\ln \frac{y}{1-y}=\theta^{T} x,$ 若将 $y$ 视为样本 $x$ 作为正例的可能性, 则 $1-y$ 是其反例的可能性, 两者的比值 $\frac{y}{1-y}$ 称为几率 $(\mathrm{odds}),$ 反映了 $x$ 作为正例的相对可能性。对几率取对数则得到了对数几率 (log odds,亦称logit),将 $y$ 视为后验概率估计,重写公式有:
由式$(8)$可得:
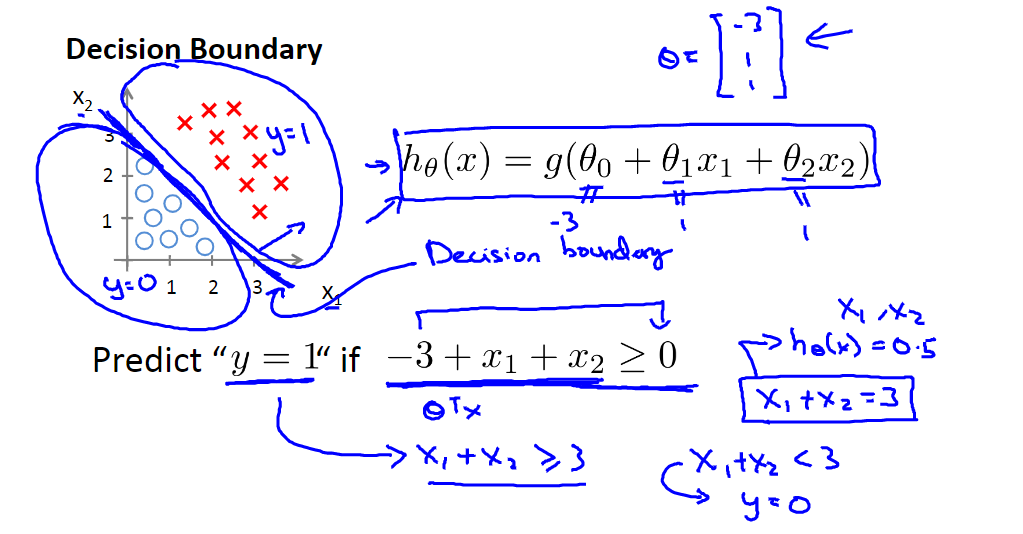
二、决策边界(Decision Boundary)
| 决策边界 | 非线性决策边界 |
|---|---|
 |
 |
三、代价函数(Cost Function)
确定逻辑回归的数学形式后, 接下来需要做的就是给定训练集, 通过最小化代价函数, 找出模型的最优参数 $\theta_{\circ}$ 线性回归中的代价函数:
我们可以类比线性回归, 使用平均误差平方来作为代价函数。
但是对于逻辑回归而言, $h_{\theta}(x)$ 函数 $\left(h_{\theta}(x)=\frac{1}{1+e^{-\theta T_{x}}}\right)$ 是一个非常复杂的非线性救, 如果将 $\operatorname{Sigmoid}$ 函数带入式 $(9),$ 并画出 $J(\theta)$ 的图像, 你会发现 $J(\theta)$ 是个非凸函数, 这就意味代价函数有着许多的局部最小值, 如下图non-convex所示, 如果将梯度下降法应用到该函数上, 无法保证可以收敘到最小值, 这很不利于我们的求解。
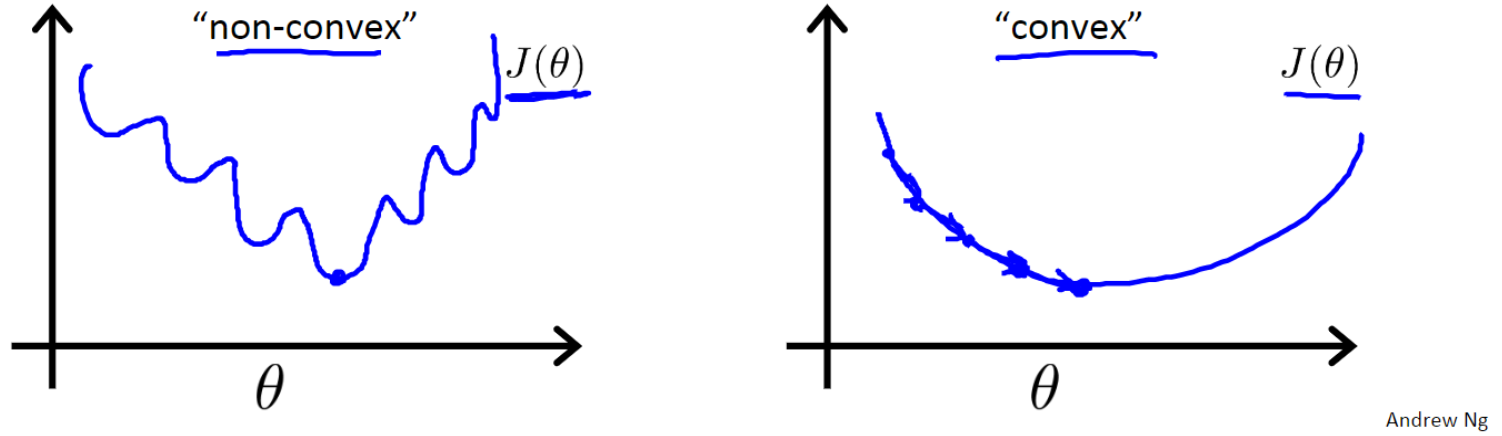
因此,通常使用极大似然估计来求解,即找到一组参数,使得在这组参数下,我们数据的似然度(概率)最大。
式$(11)$可以写成一般形式:
使用极大似然估计得到似然函数:
为了方便求解,对式$(13)$两边同时取对数,得:
现在的目标是使得$l(\theta)$最大,则在其基础上使用梯度下降法求解$-l(\theta)$的最小值即可:
为了更好的理解推导出的代价函数,可以写出代价$Cost(h_\theta(x),y)$与$h_θ$的关系函数:
即:
绘制该函数图像:
| $−ln(h_\theta(x))$ | $−ln(1−h_\theta(x))$ |
|---|---|
 |
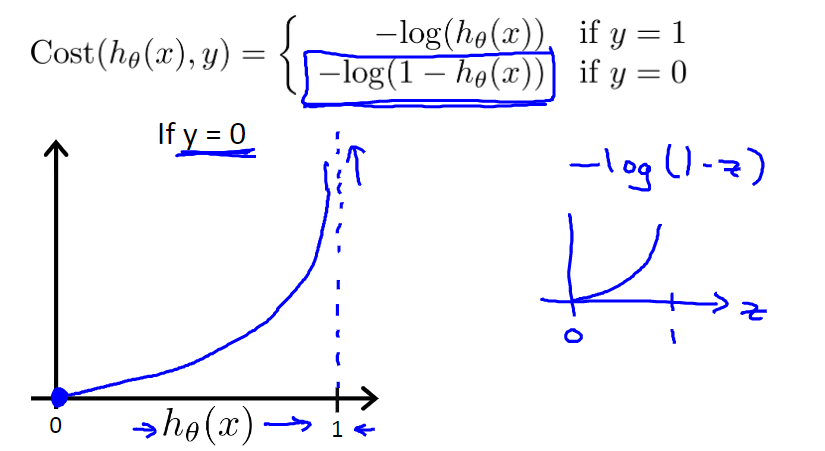 |
从上图可以看出,如果样本值$y$为$1$的话,预测值$h_\theta(x)$越接近$1$损失越小,反之越大;同样,如果样本值$y$为$0$的话,预测值$h_\theta(x)$越接近0损失越小,反之越大。
四、使用梯度下降法求解
对式$(5)求导不难发现,$Sigmoid$函数有一个特性,即:
使用梯度下降法需要先求解梯度:
公式最终简化如下如下:
梯度下降法更新权重:
或:
1 | # calculation J |
五、解决多分类问题
我们已经知道,逻辑回归(对数几率回归, Logistic Regression)只能用于解决二分类问题(Binary Classification),想要解决多分类问题,就需要对逻辑回归进行改进。
有两种方法可以使得逻辑回归解决多分类任务:
- 将多分类问题拆分为多个二分类问题,利用逻辑回归分类器进行投票求解。
- 改进逻辑回归的损失函数,使其不再只考虑二分类非1就0的损失,而是具体考虑每个样本的损失,这种方法被称为
SoftMax回归。
5.1 One vs Rest
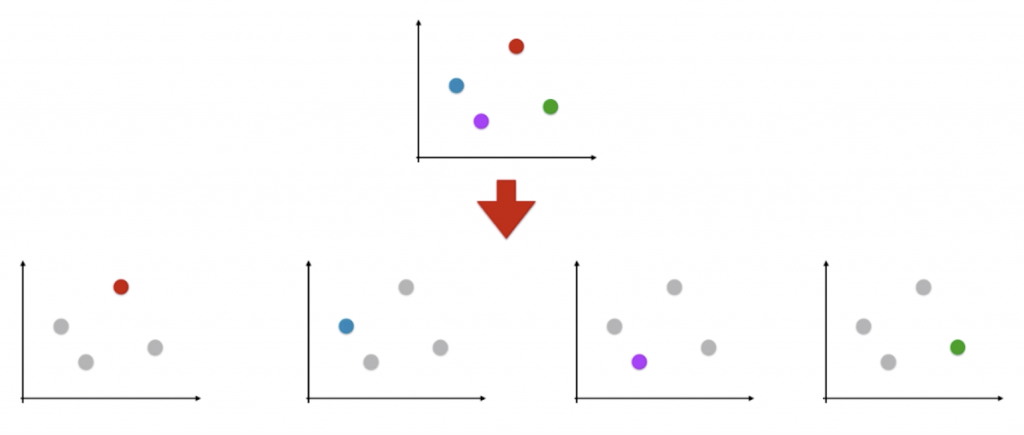
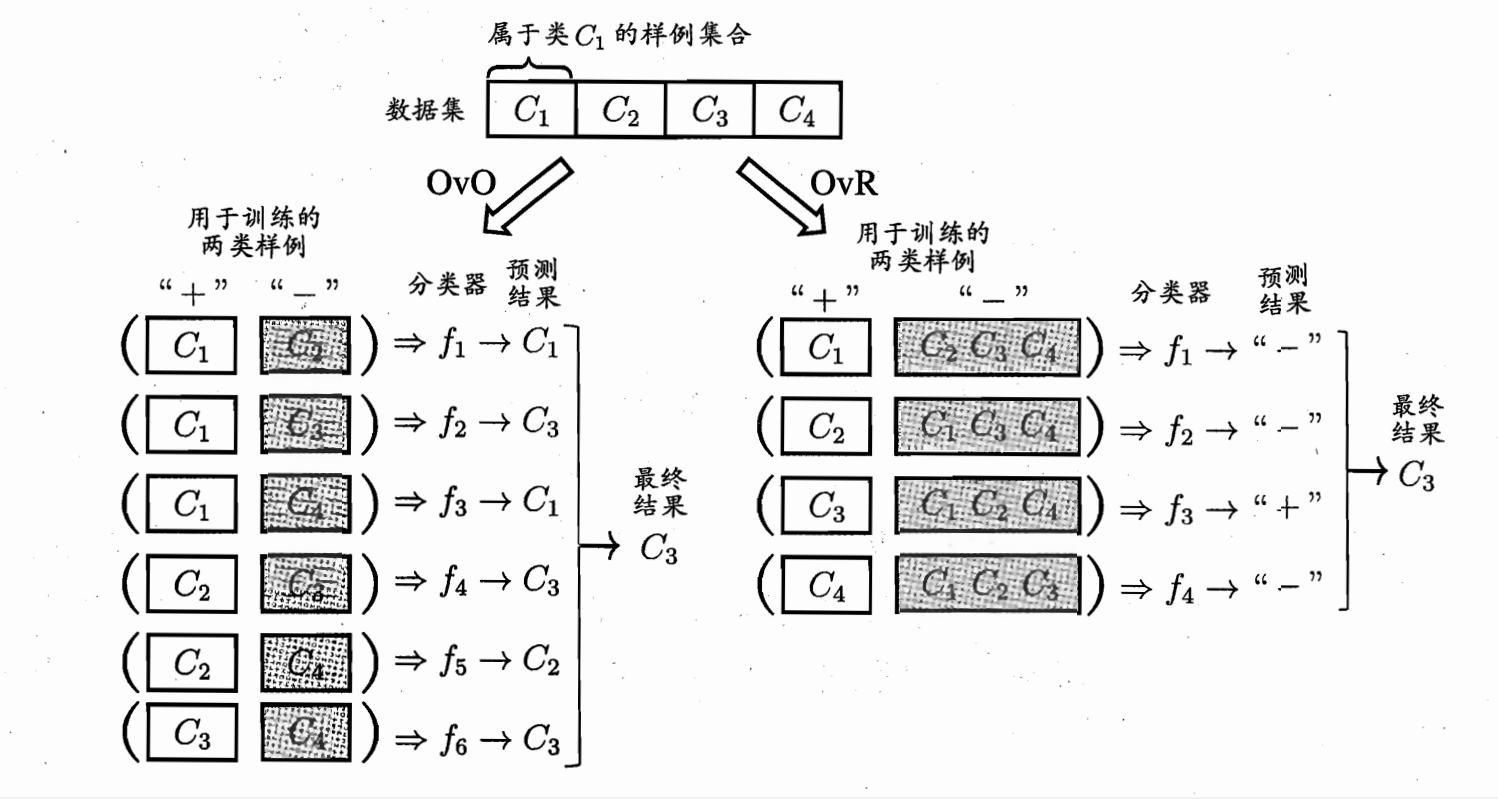
思想:假设对n种类型的样本进行分类,依次将其中某一类当作正类(positive),其他剩余的样本归为负类(negtive),训练n个二元分类器,将待测样本传入这n个分类器中,得概率最高的那个分类器对应的样本类型即认为是该预测样本的类型。
1 | def one_vs_rest(self, X, y, num_labels, learning_rate=1e-3, num_iters=100, batch_size=200, verbose=True): |
5.2 One vs One
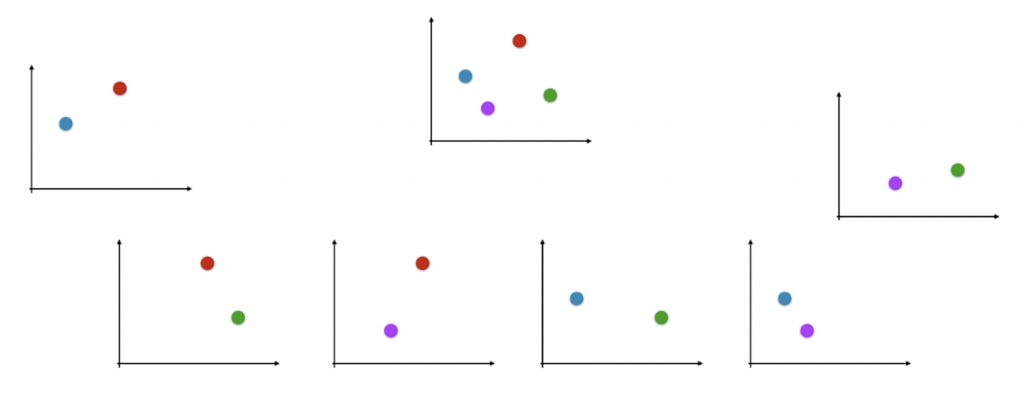
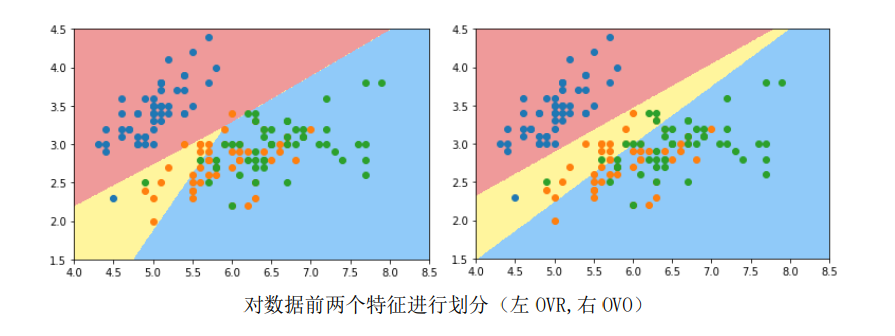
思想:对n种类型的样本进行分类,每次选出22种类型,两两结合,一共有$C_2^n$种二分类情况,使用 $C_2^n$种模型预测样本类型,对预测结果进行投票,出现次数最多的样本类型,即为该样本最终的预测类型。
六、手写数字识别


