机器学习方法(四)：决策树（Decision Tree）

一、什么是决策树？

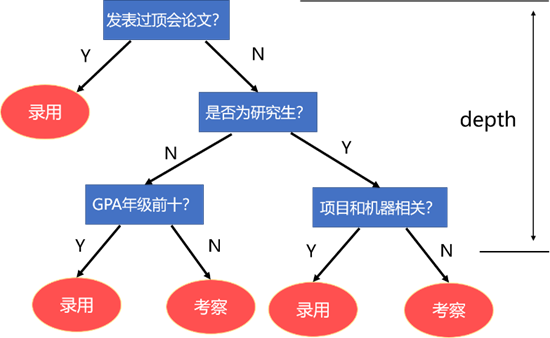
假如某公司想招聘机器学习的算法工程师，则可能会首先判断是否发表过顶会论文，如果发表过，可能会考虑录用。倘若没有，则继续判断是否为研究生，若是研究生，就看他研究生期间有没有做过有关机器学习的项目，若有，可能会考虑录用，若没有，则再进行考察。若不是研究生，则判断他的$GPA$是否年级前十…

每次的判断都相当于一次决策，每次决策逐渐累积构成了一棵树，即为决策树。而决策树学习目的就是为了产生一颗泛化能力强，即处理未见数据强的决策树。

1.1 信息熵

“信息熵”是度量样本集合纯度的一种指标，也为随机变量的不确定度的度量。假定当前样本集合$D$中第$k$类样本所占比例为$p_{k}(k=1,2,3 \ldots N)$，则$D$的信息熵定义为：

$$\operatorname{Ent}(D)=-\sum_{k=1}^{|y|} p_{k} \log _{2} p_{k}$$

$\operatorname{Ent}(D)$的值越小，集合$D$的纯度越高，不确定度越低，确定性越强。

例如：当$D_1=\left\{\frac{1}{3}, \frac{1}{3}, \frac{1}{3}\right\}$时，$D_1$的信息熵$\operatorname{Ent}\left(D_{1}\right)=-\frac{1}{3} \log _{2}\left(\frac{1}{3}\right)-\frac{1}{3} \log _{2}\left(\frac{1}{3}\right)-\frac{1}{3} \log _{2}\left(\frac{1}{3}\right)=1.5846$

当$D_2=\left\{\frac{1}{10}, \frac{2}{10}, \frac{7}{10}\right\}$}时，$D_2$的信息熵$\operatorname{Ent}\left(D_{2}\right)=-\frac{1}{10} \log _{2}\left(\frac{1}{10}\right)-\frac{2}{10} \log _{2}\left(\frac{2}{10}\right)-\frac{7}{10} \log _{2}\left(\frac{7}{10}\right)=1.15678$

显然集合$D_2$的信息熵是低于集合$D_1$的，从集合$D_2$的样本也可看出，数据更偏向于比例为$\frac{7}{10}$的类别，确定性更大，不确定性小。而集合$D_1$的三种类别比例相同，不确定性更大。

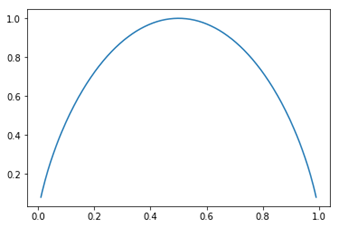
以二分类为例，信息熵$\operatorname{Ent}(D)=-x \log _{2} x-(1-x) \log _{2}(1-x)$，函数图像如上图所示。

可以看出，当$x$趋向于两端时，也即数据倾向于一类时，整个集合的不确定性越小，信息熵越小。

1.2 信息增益

假设离散集$a$有$V$个可能的取值$\left\{a^{1}, a^{2}, a^{3}, \ldots, a^{V}\right\}$，其中第$v$个分支包含的集合记为$D^v$,该分支所占的权重记为，$\frac{|D^{v}|}{|D|}$样本越多的分支节点影响越大，下面即可计算出属性$a$对样本集$D$进行划分所产生的信息增益为：

$$\operatorname{Gain}(D, a)=\operatorname{Ent}(D)-\sum_{v=1}^{|y|} \frac{\left|D^{v}\right|}{|D|} \operatorname{Ent}\left(D^{v}\right)$$

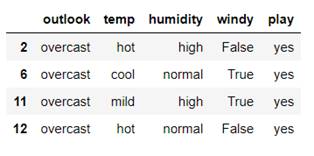
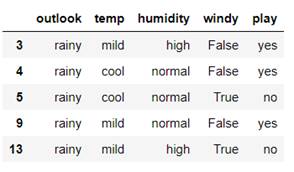
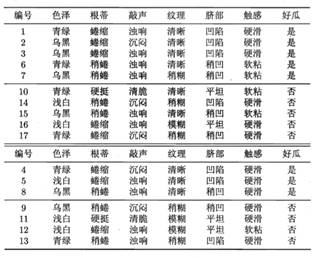
对于以下的$tennis$数据（下图），根据天气、温度、湿度、是否有风决定是否打网球，使用信息熵、信息增益来构造该数据的决策树：

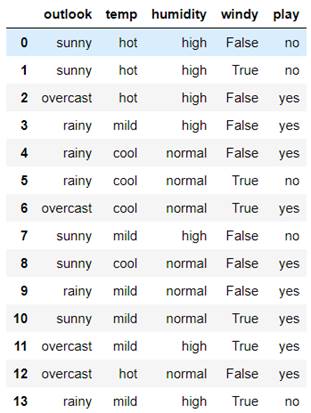
对于$outlook$决策分支的数据，有$sunny、overcast、rainy$三个分支（右侧三组数据），分别计算三类数据的信息熵：

$$\text { Ent }(\text { sunn } y)=-\sum_{i=1}^{n} p_{i} \log _{2} p_{i}=-\left(\frac{2}{5} \log _{2} \frac{2}{5}+\frac{3}{5} \log _{2} \frac{3}{5}\right) \approx 0.971$$

$$\text { Ent(overcast) }=-\sum_{i=1}^{n} p_{i} \log _{2} p_{i}=-\left(\log _{2} 1\right)=0$$

$$\text { Ent }(\text { rainy })=-\sum_{i=1}^{n} p_{i} \log _{2} p_{i}=-\left(\frac{3}{5} \log _{2} \frac{3}{5}+\frac{2}{5} \log _{2} \frac{2}{5}\right) \approx 0.971$$

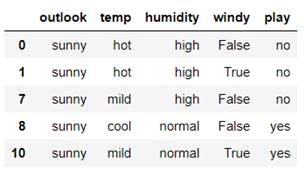
计算未划分前的信息熵

$$\text { Ent }(\text { Play })=-\sum_{i=1}^{n} p_{i} \log _{2} p_{i}=-\left(\frac{9}{14} \log _{2} \frac{9}{14}+\frac{5}{14} \log _{2} \frac{5}{14}\right) \approx 0.940$$

计算使用$outlook$划分造成的信息增益：

$$\begin{array}{c} \text { Gain }(\text { Play, Outlook })=\text { Ent }(\text { Play })-\frac{5}{14} \text { Ent }(\text { sunny })-\frac{4}{14} \text { Ent }(\text { overcast })-\frac{5}{14} \text { Ent }(\text { rainy }) \\ =0.940-0.347-0-0.347=0.2467 \end{array}$$ $$\text { Ent }(\text { rainy })=-\sum_{i=1}^{n} p_{i} \log _{2} p_{i}=-\left(\frac{3}{5} \log _{2} \frac{3}{5}+\frac{2}{5} \log _{2} \frac{2}{5}\right) \approx 0.971$$

同理计算使用$temp、humidity、windy$分支进行划分所产生的信息增益：

• $Gain(Play, Temperature) - 0.029$
• $Gain(Play, Humidity) - 0.151$
• $Gain(Play, Wind) - 0.048$

由上述可得，使用$outlook$进行划分所产生的信息增益最大，所以以天气为根节点，并判断信息熵不为零，需要继续向下划分。所以首先使用$outlook$进行划分：

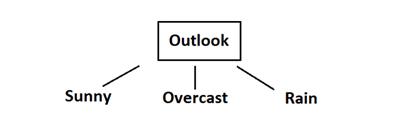
接着使用同样的方法继续寻找$Sunny$分支中的最优划分属性：

• $Gain(Sunny, Humidity) - 0.970951$
• $Gain(Sunny, Windy) - 0.019973$
• $Gain(Sunny, Temperature) - 0.570951$

$Sunny$分支使用$Humidity$进行划分产生的信息增益最大，故使用$Humidity$进行划分。

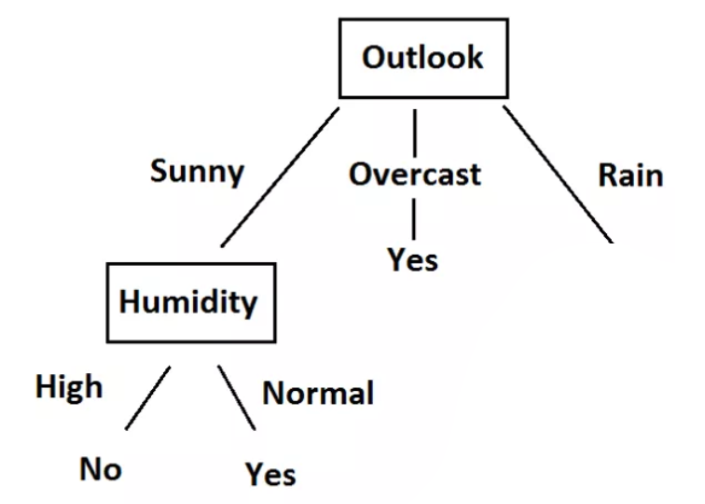
同时可以计算出此时湿度对应的信息熵high、normal均为0，所以当湿度为high时，决定No；当湿度为normal时，决定Yes；此时它就是叶子节点。当天气为Overcast时，根据信息可知，最终决定为Yes。因此，它就是叶子节点。

接着使用同样的方法继续寻找$Rain$分支中的最优划分属性：

• $Gain(Rainy, Temperature) - 0.019973$
• $Gain(Rainy, Wind) - 0.970951$

当天气为$Rainy$时信息增益最大的是$Windy$，因此在$Rainy$下通过$Windy$来进行划分。同时，当$Windy$为$True$时决定为$No$，当分为False时决定为$Yes$。

$Overcast$分支数据已经属于同一类别，故不再做划分。最终构造出的决策树：

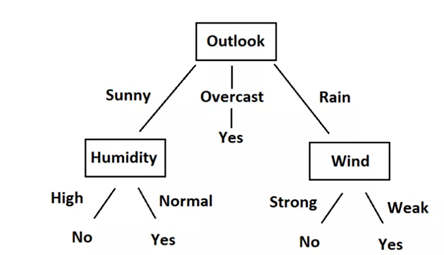
1.3 基尼系数

分类问题中，假设有k​个类，样本点属于第​k​类的概率为$𝑝_𝑘$，则概率分布的基尼系数为:

$$\operatorname{Gini}(D)=\sum_{k=1}^{|y|} \sum_{k^{\prime} \neq k} p_{k} p_{k}^{\prime}=1-\sum_{k=1}^{|y|} p_{k}^{2}$$

直观来讲，$Gini(D)$反映了从数据集$D$中随机抽取两个样本，其类别标记不一致的概率。因此$Gini(D)$越小，数据集的纯度越高。信息熵的计算比基尼系数计算要慢，但大多数情况下两者没有太大区别。

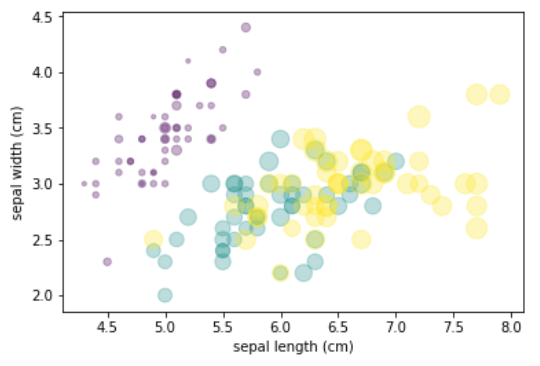
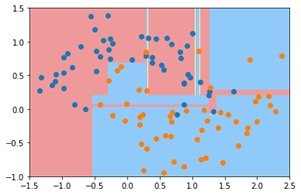
决策树不像线性回归、逻辑回归，需要$OVR、OVO$思想才能解决多分类问题。决策树天生就可解决多分类问题，下图是使用决策树分类器对鸢尾花数据集（后两个特征）进行分类的结果：

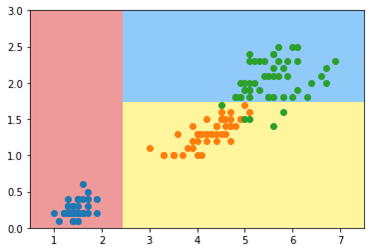
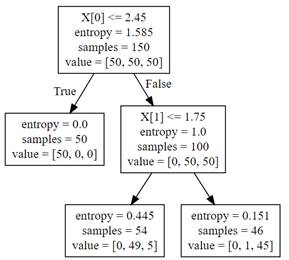
二、决策树

2.1 鸢尾花数据集

鸢尾花数据集是模式识别、机器学习等领域里使用较多的一个数据集，数据集共收集了三类鸢尾花，即Setosa​鸢尾花、Versicolour鸢尾花和Virginica鸢尾花，每一类鸢尾花收集了50条样本记录，共计150条。数据集包括4个属性，分别为花萼的长、花萼的宽、花瓣的长和花瓣的宽。

该数据集用于利用决策树实现分类。数据显示如下（左图）。其中包含有四个特征属性，取值均为数值型，且具有相同的量纲，第五列为通过前面四列所确定的鸢尾花所属的类别名称。将数据的两个特征表示为X轴、Y轴，第三个或第四个特征课表示为点的大小，最终的可视化数据图如下（右图）：

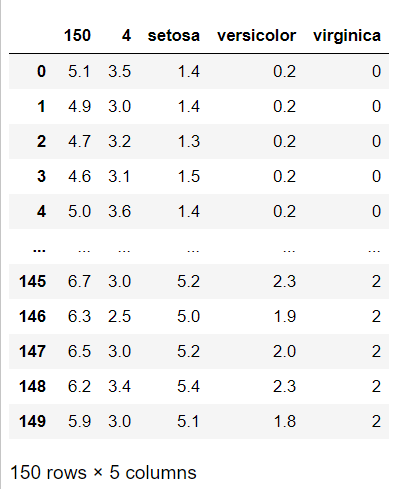
2.2 决策树构造算法

决策树有三种常用的实现算法：基于信息增益的$ID3$、基于信息增益率的$C4.5$及基于基尼指数的$CART$算法。$scikit-learn$决策树基于$CART$算法。此处用基于信息增益的$ID3$算法生成决策树。信息增益表示信息不确定性的减少程度，即信息增益越大，信息的确定性越高，故而选取信息增益最大的属性作为决策特征。

通过所给数据集的相应特征求得经验熵和经验条件熵，再利用公式计算信息增益。重复进行，直到所有样本都做出了最终决策并生成完整决策树。

2.2.1 $ID3$算法

$ID3$算法的核心是在决策树各个结点上应用信息增益准则选择特征，递归地构建决策树。

具体方法是：从根结点(root node)开始，对结点计算所有可能的特征的信息增益，选择信息增益最大的特征作为结点的特征，由该特征的不同取值建立子结点;再对子结点递归地调用以上方法，构建决策树;直到所有特征的信息增益均很小或没有特征可以选择为止。最后得到一棵决策树。$ID3$相当于用极大似然法进行概率模型的选择。

2.2.2 $C4.5$算法

$C4.5$是一系列用在机器学习和数据挖掘的分类问题中的算法。它的目标是监督学习：给定一个数据集，其中的每个元组都能用一个属性值来描述，每一个元组属于一个互斥的类别中的某一类。

$C4.5$的目标是通过学习，找到一个从属性值到类别的映射关系，并且这个映射能用于对新的类别未知的实体进行分类。$C4.5$算法与$ID3$算法相似，$C4.5$ 算法对$ID3$算法进行了改进。$C4.5$在生成的过程中，用信息增益比来选择特征。

2.2.3 $CART$算法

$CART(Classification And Regression Tree)$算法采用一种二分递归分割的技术，将当前的样本集分为两个子样本集，使得生成的的每个非叶子节点都有两个分支。因此，$CART$算法生成的决策树是结构简洁的二叉树。

2.3 核心算法描述

2.3.1 信息熵、信息增益的计算

（1）计算数据集$D$的信息熵$H(D)$：

$$H(D)=-\sum_{k=1}^{K} \frac{\left|C_{k}\right|}{|D|} \log _{2} \frac{\left|C_{k}\right|}{|D|}$$

def _calc_entropy(self, y):
    """ 计算信息熵
    y: 数据集标签
    """
    entropy = 0
    # 计算每个类别的数量
    _, num_ck = np.unique(y, return_counts=True)
    for n in num_ck:  # 找到每个类别的数量
        p = n / y.shape[0]
        entropy -= p * np.log2(p)  # 计算信息熵
    return entropy

（2）计算特征$A$对数据集$D$的经验条件熵$H(D|A)$：

$$H(D \mid A)=\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} H\left(D_{i}\right)=-\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} \sum_{k=1}^{K} \frac{\left|D_{i k}\right|}{\left|D_{i}\right|} \log _{2} \frac{\left|D_{i k}\right|}{\left|D_{i}\right|}$$

def _calc_condition_entropy(self, X, y):
    """ 计算条件熵  x: 数据集的某个特征对应的列向量，列表示特征
    y: 数据集标签 """
    cond_entropy = 0  # 初始化条件熵为0
    # 计算特征x可能的取值及对应出现的次数
    xval, num_x = np.unique(X, return_counts=True)
    for V, n in zip(xval, num_x):  # 遍历该特征的每个值
        y_sub = y[X == V]  # 该值所对应的划分，相当于把对应值取出来
        sub_entropy = self._calc_entropy(y_sub)  # 计算分支的熵
        p = n / y.shape[0]  # 计算每分支所占比例
        cond_entropy += p * sub_entropy  # 求和
    return cond_entropy

（3）计算数据$D$使用特征$A$划分后所产生的信息增益,即划分前的信息熵-划分后的条件熵：

$$g(D, A)=H(D)-H(D \mid A)$$

def _calc_gain_entropy(self, X, y):
    """ ID3算法 计算信息增益
    x: 数据集的某个特征对应的列向量，训练集中一行表示一个样本，列表示特征  y: 数据集标签  """
    return self._calc_entropy(y) – self._calc_condition_entropy(X, y)

2.3.2 ID3算法

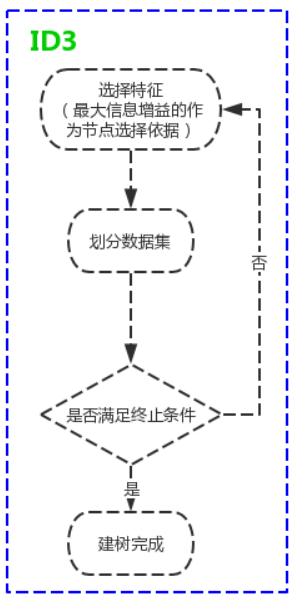
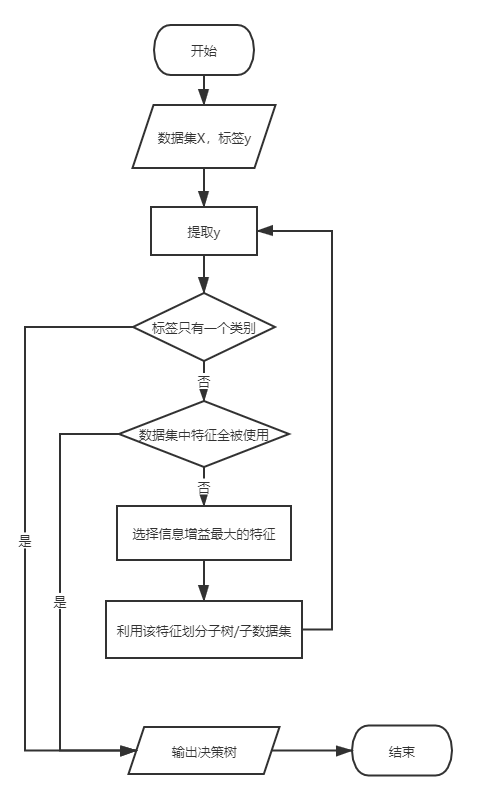
ID3算法的核心是在决策树各个结点上应用信息增益准则选择特征，递归的构造决策树。构造决策树T的过程：

输入：训练数据集D、特征集A、阈值𝜖

输出：决策树T

• 1. 若当前数据𝐷中所有实例属于同一类𝐶𝑘，则𝑇为叶节点，并将该类别𝐶𝑘作为当前叶节点的类别，返回𝑇；
  2. 若𝐴=空集，则𝑇为单结点树，并将𝐷中实例数最大的类𝐶𝑘（进行投票）作为该结点的类标记，返回𝑇；
  3. 否则，计算𝐴中各个特征对数据𝐷的信息增益，选择信息增益最大的特征𝐴𝑔；
  4. 如果𝐴𝑔的信息增益小于阈值𝜀，则置𝑇为叶节点，并将D中实例数最大的类𝐶𝑘（进行投票）作为该结点的类标记，返同𝑇；
  5. 否则，对𝐴𝑔每一可能值𝑎𝑖，依𝐴𝑔=𝑎𝑖将𝐷分割为若干非空子集𝐷𝑖，将𝐷𝑖中实例数最大的类作为标记（进行投票），构建子结点，由结点及其子结点构成树𝑇，返回𝑇；
  6. 对第𝑖个子结点，以𝐷𝑖为训练集，以𝐴−{𝐴𝑔}为特征集，递归地调用过程（1）∼过程（5），得到子树𝑇𝑖，返回𝑇𝑖。

2.3.3 C4.5算法

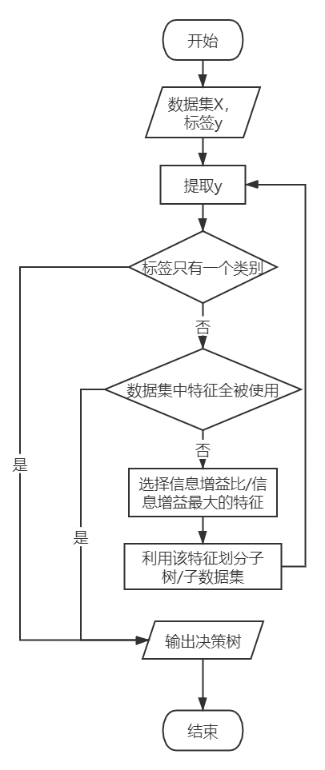
C4.5算法对ID3算法进行了改进。C4.5在生成的过程中采用信息增益比/率来选择特征。

信息增益比：特征 A对训练数据集D的信息增益比𝑔𝑅(𝐷,𝐴)定义为其信息增益𝑔(𝐷,𝐴)与训练数据集𝐷关于特征𝐴的值的熵𝐻𝐴(𝐷)之比,即：

$$g_{R}(D, A)=\frac{g(D, A)}{H_{A}(D)} \quad H_{A}(D)=-\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} \log _{2} \frac{\left|D_{i}\right|}{|D|}$$

其中，𝑛表示的是特征𝐴取值的个数。

def _calc_gain_ration(self, X, y):
    """ C4.5 计算信息增益率/比
    x: 数据集的某个特征对应的列向量，训练集中一行表示一个样本，列表示特征
    y: 数据集标签
    """
    return self._calc_gain_entropy(X, y) / self._calc_entropy(X)

2.3.4 CART算法（分类树）

决策树的生成就是递归地构建二叉决策树的过程。对回归树使用平方误差最小化准则，对分类树用基尼指数 (Gini index) 最小化准则，进行特征选择，生成二叉树。

基尼系数：分类问题中，假设有K个类，样本点属于第𝑘类的概率为𝑝𝑘,则概率分布的基尼系数定义为：

$$\operatorname { Gini } ( p ) = \sum _ { k = 1 } ^ { K } p _ { k } \left( 1 - p _ { k } \right) = 1 - \sum _ { k = 1 } ^ { K } p _ { k } ^ { 2 }$$

对于二分类问题，若样本点属于第1个类的概率是p，则概率分布的基尼系数为:

$$\operatorname { Gini } ( p ) = 2 p ( 1 - p )$$

对于给定的样本集合D，其基尼系数为：

$$\operatorname { Gini } ( D ) = 1 - \sum _ { k = 1 } ^ { K } \left( \frac { \left| C _ { k } \right| } { | D | } \right) ^ { 2 }$$

def _calc_evaluation(self, y):
    """ 计算标签为y的数据集的基尼指数 """
    # 计算每个类别样本的个数
    _, num_ck = np.unique(y, return_counts=True)
    gini = 1
    for n in num_ck:
        gini -= (n / y.shape[0]) ** 2
    return gini

CART算法构造决策二叉树T的过程：

1. 设结点的训练数据集为$𝐷$，计算现有特征对该数据集的基尼指数。此时，对每一个特征$𝐴$，对其可能取的每个值$𝑎$，根据样本点对$𝐴=𝑎$的测试为“是”或“否”将$𝐷$分割成$𝐷_1$和$𝐷_2$两部分；
2. 在在所有可能的特征$𝐴$以及它们所有可能的切分点$a$中，选择基尼系数最小的及其对应的切分点作为最优特征与最优切分点。依最优特征与最优切分点，从现结点生成两个左右子结点，将训练数据集依据特征分配到两个子结点中去。
3. 对其左右子结点递归的调用过程(1)、(2)，直至满足停止条件。
4. 返回生成的CART决策二叉树。

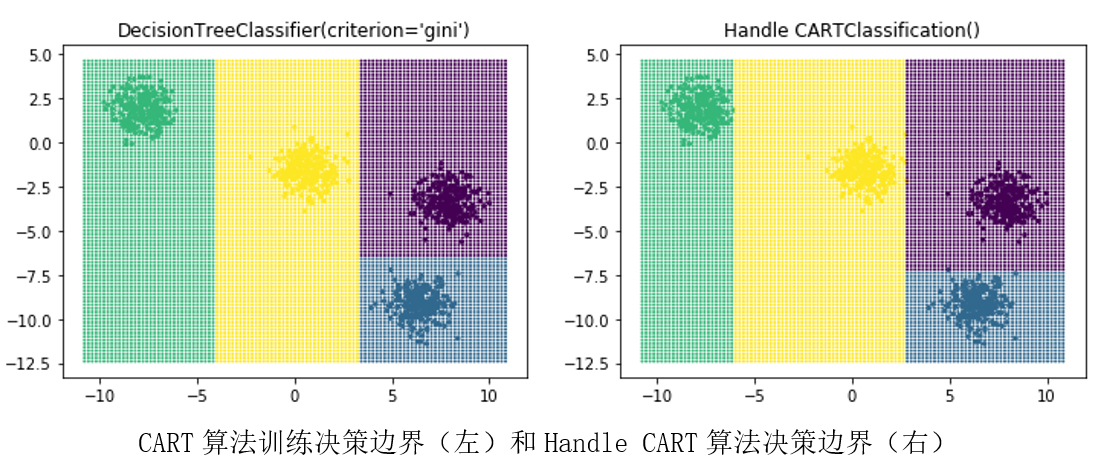
使用sklearn中的CART决策树分类器和自己实现的分类树，对聚类数据划分决策边界，并进行对比。可以发现库函数中的分类器是要优于我们自己的决策树分类器。

2.3.5 CART算法（回归树）

假设 $X$ 与$Y$分别为输入和输出变量，并且$Y$是连续变量，给定训练数据集：

$$D = \left\{ \left( x _ { 1 } , y _ { 1 } \right) , \left( x _ { 2 } , y _ { 2 } \right) , \cdots , \left( x _ { N } , y _ { N } \right) \right\}$$

一棵回归树对应着输入空间 (即特征空间) 的一个划分以及在划分的单元上的输出值。假设已将输入空间划分$M$个单元$R_1, R_2,……, R_m$，并且在每个单元$R_m$上有一个固定的输出值$C_m$,于是回归树模型可表示为：

$$f ( x ) = \sum _ { m = 1 } ^ { M } c _ { m } I \left( x \in R _ { m } \right)$$

def _calc_division(self, y_left, y_right):
    """计算划分后的平方差"""
    # 计算左右子树平方差
    left_evaluation = self._calc_evaluation(y_left)
    right_evaluation = self._calc_evaluation(y_right)
    # 划分后的平方差
    after_divide = left_evaluation + right_evaluation
    return after_divide

def _calc_evaluation(self, y):
    """计算平方差"""
    return np.sum(np.power(y - np.mean(y), 2))

def _calc_node_val(self, y):
    """回归树返回标签的平均值作为叶结点的预测值"""
    return np.mean(y)

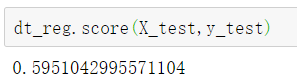
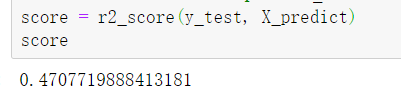
当输入空间的划分确定时，可以使用平方误差来表示回归树对于训练数据的预测误差，用平方误差最小的准则求解每个单元上的最优输出值。使用回归树对波士顿房价进行预测，并计算库函数中的回归树训练准确率对比，优化回归树准确率（左）和优化回归树准确率（右）：

三、剪枝

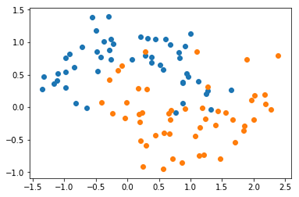
决策树分类器默认是认为信息熵为$0$时才停止划分, 极易产生过拟合现象。如下图所示，有时候会因为迁就一个或几个点，而去产生新的决策，从而导致整个决策树非常庞大，这时候就需要进行剪枝操作，即“剪”掉不必要的分支。

3.1 预剪枝

每次划分前后，都要对这次的划分进行评估，下图即使用验证集来计算划分前后的分类准确率，只有在准确率时的划分才可进行，否则禁止划分。

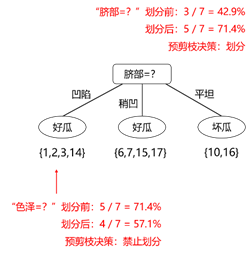
3.2 后剪枝

与预剪枝不同，后剪枝是先从训练集生成一颗完整的决策树，然后根据验证集准确率来进行剪枝。即对决策树的非叶子节点，从下到上，使用其领衔的分支进行替换，然后计算剪枝前后的验证集准确率，若有提升，则进行剪枝。

四、问题及解决办法

• 如何判断决策树的泛化能力是否得到提升？

使用验证集对其进行测试。

• 如果属性值是连续的怎么办？

此时可采用连续属性离散化的技术，简单的策略就是二分法。将连续属性出现的样本对应的值按升序排列，然后取相邻两个值之间的中点作为一个离散点进行划分。

• 如果样本的属性值缺失了如何处理？

① 在选择划分属性时，可使用那个属性值完整的样本进行选择

② 为每一个样本定义一个权重，若样本在该属性处未发生缺失，则按照相应的属性值进入下一个子结点，权重不发生改变；若发生缺失，则划入所有子结点，并更新其权重

• 训练过程中如何防止过拟合？

剪枝是决策树中防止过拟合的主要方法。大致分为预剪枝和后剪枝两种。预剪枝是在决策树的生成过程中，对每个结点在划分前进行估计，若当前结点的划分不能带来决策树泛化能力的提升，则停止划分并将当前结点标记为叶结点。后剪枝则是先从训练集生成一颗完整的决策树，然后自底向上地对非叶子结点进行考察，若将该结点对应的子树替换为叶结点能提升泛化能力，则进行替换。

Reference

• 《机器学习》 周志华著

赏

谢谢你请我吃糖果

支付宝

微信