机器学习方法(五)：正则化

2019-08-04

× 文章目录

1. 一、过拟合问题
2. 二、正则化
1. 2.1. 2.1 L1正则项（lasso回归）
  1. 2.1.1. 2.1.1 直观理解（权重使用$w$表示）
2. 2.2. 2.2 L2正则化（岭回归）
  1. 2.2.1. 2.2.1 直观理解（权重使用$w$表示）
3. Reference

一、过拟合问题

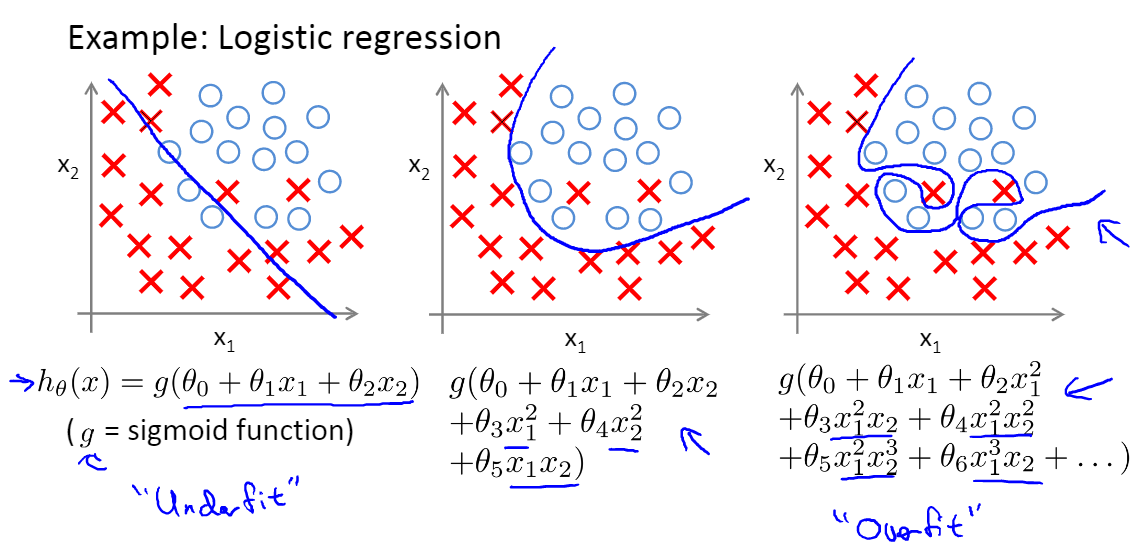
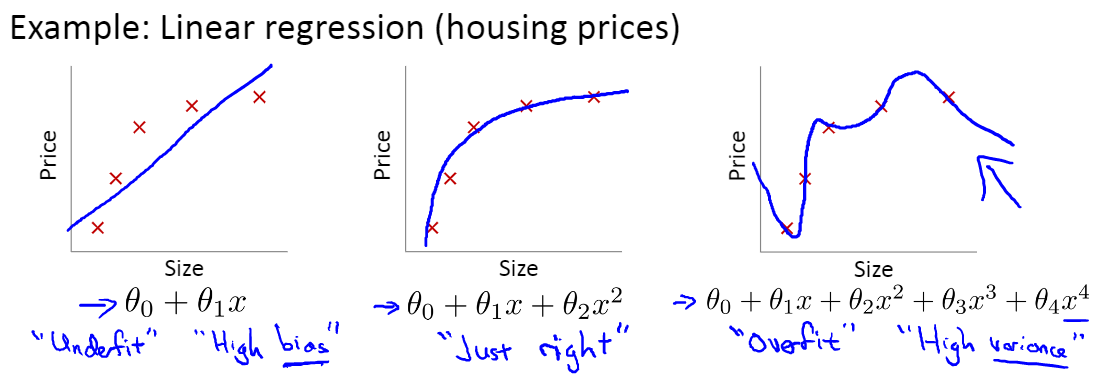
指的是我们设计的模型过度拟合训练集$J(\theta)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2} \approx 0$，导致它在训练集上表现很好，但是在测试集上却表现很差，无法泛化到新的样本中，难以对新样本进行预测。

那么如何预防过拟合？

减少特征的数量

人工选择哪些特征应该保留，那些应该舍弃；

模型选择算法（Model selection algorithm）；

正则化

保留所有的特征，但减小参数$(\theta_j)$的幅值；

当数据有很多特性时，每个特性都对预测y有一点贡献；

二、正则化

即在原目标（代价）函数中添加惩罚项，对复杂度高的参数进惩罚，从而减小模型的复杂度。改进后的代价函数数学表达形式为：

$\begin{equation} \tilde{J}(\theta ; X, y)=J(\theta ; X, y)+\lambda \Omega(\theta) \tag{1} \end{equation}$

2.1 L1正则项（lasso回归）

在原始的损失函数后面加上一个$L1$正则化项，即全部权重的绝对值的和，再乘以$\lambda / n$。即式(1)中$\Omega(\theta) = |\theta|$，损失函数变为：

$\begin{equation} \tilde{J}(\theta ; X, y)=J(\theta ; X, y)+\frac{\lambda}{n}\sum_{i=1}^n |\theta_i| \tag{2} \end{equation}$

对其求导，可得：

$\frac{\partial \tilde{J}(\theta)}{\partial \theta} = \frac{\partial J(\theta)}{\partial \theta} + \frac{\lambda}{n} sign(\theta), 其中\operatorname{sign}(\theta)=\left\{\begin{array}{l}1, \theta>0 \\0, \theta=0 \\-1, \theta<0\end{array}\right.$

梯度下降时，权重更新：

$\theta_{j}:=\theta_{j}-\alpha \frac{\partial J(\theta)}{\partial \theta} - \frac{\alpha\lambda}{n}sign(\theta)$

不难看出，当$\theta=0$ 时，$|\theta|$是不可导的，仍然以未正则化的梯度更新$\theta$；

当$\theta>0$ 时，$sign(\theta)>0$，即梯度下降法更新后$\theta$变小；

当$\theta<0$ 时，$sign(\theta)<0$，即梯度下降法更新后$\theta$变大；综上所述，说明$L1$正则化使得权重（参数）$\theta$向0趋近，使得网络中的权重（参数）尽可能为0，减小了模型的复杂度。

2.1.1 直观理解（权重使用$w$表示）

考虑带约束条件的优化解释:

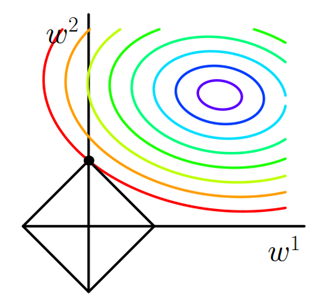
$\begin{array}{c}\min _{w} J(w ; X, y) \\\text { s.t. }\|w\|_{1} \leq C\end{array}$ 直观理解L1正则化

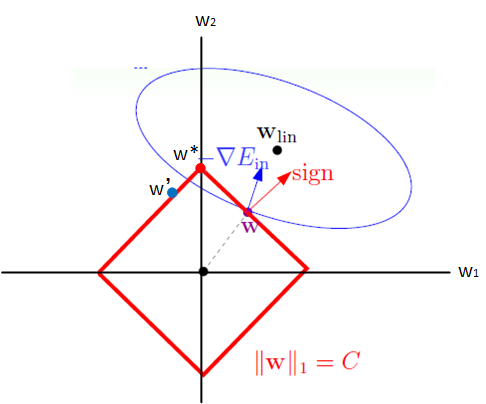
假设X为二维样本，由右图可以理解，$w$点朝着$\nabla J(w)$在切线方向的分量沿着边界向左上移动，当到达$w’$时，$\nabla J(w)$在切线方向的分量变为右上方。直到$w$稳定在顶点处，达到最优解$w^*$。此时，$w_1=0$，这也解释了会使权重变得稀疏的原因。

如果不加L1正则化，目标函数为凸函数的话，梯度下降的结果就是最里边的紫色等高线内部的某一点。
若加入L1正则化，那么目标是不仅是原曲线的值要小，还要使得这个菱形越小越好。

线性回归、逻辑回归中带有$L1$正则化项的代价函数：
$J(\theta)=\frac{1}{2 m}\left[\sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}+\lambda \sum_{j=1}^{n} |\theta_{j}|\right]$

2.2 L2正则化（岭回归）

在原始的损失函数后面加上一个$L2$正则化项，即全部权重的平方和，再乘以$\lambda / 2n$。则损失函数变为：

$\begin{equation} \tilde{J}(\theta ; X, y)=J(\theta ; X, y)+\frac{\lambda}{2n}\sum_{i=1}^n \theta_i^2 \tag{2} \end{equation}$

对应的梯度：

$\begin{aligned} \frac{\partial \tilde{J}(\theta)}{\partial \theta} &= \frac{\partial J(\theta)}{\partial \theta} + \frac{\lambda}{n} \theta, \theta = [\theta_1,\theta_2,\theta_3,...,\theta_n] \\ \frac{\partial \tilde{J}(\theta)}{\partial \theta_0} &= \frac{\partial J(\theta)}{\partial \theta_0}\\ \end{aligned}$

$L2$正则化项对偏置 $\theta_0$ 的更新没有影响，可是对于权重 $\theta = [\theta_1,\theta_2,\theta_3,…,\theta_n]$的更新有影响：

$\begin{aligned} & \text{Repeat}\{ \\ & \quad \quad \begin{aligned} \theta_{j} &:=\theta_{j}-\alpha \frac{\partial J(\theta)}{\partial \theta_j} - \frac{\alpha\lambda}{n}\theta_j \\ & := (1- \frac{\alpha\lambda}{n}) \theta_j - \alpha \frac{\partial J(\theta)}{\partial \theta_j}，(j=1,2,3,...,n)\\ \theta_0 &:= \theta_0 - \alpha \frac{\partial J(\theta)}{\partial \theta_0} \end{aligned} \\ & \} \end{aligned}$

由于其中$\alpha 、\lambda、n$都是大于0的，因此$1 - \frac{\alpha \lambda}{n}$是个小于1的数。所以在梯度下降的过程中权重参数$\theta$在不断减小，趋向于0但不等于0，这也是该方法也被称为权重衰减（weight decay）的原因。

2.2.1 直观理解（权重使用$w$表示）

考虑带约束条件的优化解释

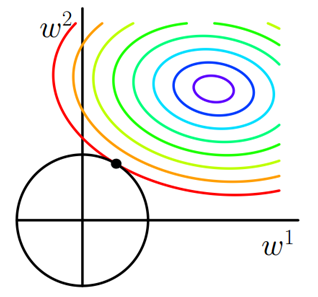
$\begin{array}{c}\min _{w} J(w ; X, y) \\\text { s.t. }\|w\|_{2} \leq C\end{array}$ 直观理解L2正则化

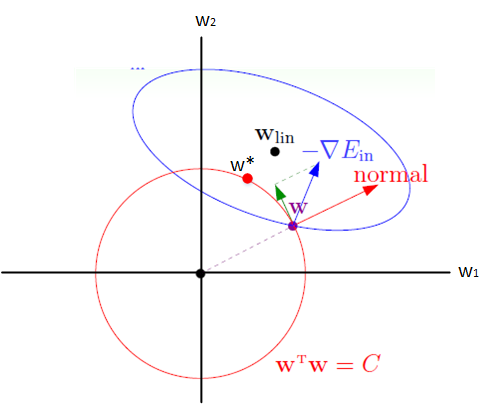
假设X为二维样本，图中椭圆为原目标函数$J(w)$的一条等高线，圆为半径为$\sqrt{C}$的范数球。由于约束条件的限制，$w$必须位于范数球内。对于边界上的一点$w$ ，图中蓝色箭头为$J(w)$点在该处的梯度方向$\nabla J(w)$ ，红色箭头为范数球在该处的法线方向。由于$w$不能离开边界（不能违反约束条件），因在使用梯度下降法更新时，只能朝$J(w)$在范数球上$w$处的切线方向更新，即图中绿色箭头的方向。

如此将沿着边界移动，当与范数球上处的法线平行时，此时$\nabla J(w)$在切线方向的分量为0，将无法继续移动，从而达到最优解$w^*$（图中红色点所示）。

线性回归、逻辑回归中带有$L2$正则化项的代价函数：
$J(\theta)=\frac{1}{2 m}\left[\sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}+\lambda \sum_{j=1}^{n} \theta_{j}^{2}\right]$
同样对$\theta$求偏导：
$\frac{\partial J(\theta)}{\partial \theta_{i}} = \frac{1}{m} \sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)}) x_{j}^{(i)}+\frac{\lambda}{m} \theta_{j}$
权重更新：
$\begin{aligned}&\text { Repeat }\{\\&\begin{array}{l} \quad \quad \rightarrow \theta_{0}:=\theta_{0}-\alpha \frac{1}{m} \sum_{i=1}^{m} \left(h_{\theta} \left(x^{(i)}\right)-y^{(i)}\right) x_{0}^{(i)} \\ \quad \quad \rightarrow \theta_{j}:=\theta_{j}-\alpha \left[\frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)}+\frac{\lambda}{m} \theta_{j}\right] = \theta_{j}(1-\alpha\frac{\lambda}{m})-\alpha \left[\frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)}\right]\\ \ \ \ 其中，线性回归时，h_\theta(x^{(i)}) = \theta^T X;\\ \quad \quad \quad 逻辑回归时， h_\theta(x^{(i)}) = sigmoid(\theta^T X);\\ \quad \quad \quad (j=0(\times), \underline{1,2,3, \ldots, n}) \\ \}\end{array}\end{aligned}$
用正规方程求解：
$\theta=\left(X^{T} X+\lambda\left[\begin{array}{ccccc}0 & & & & \\& 1 & & & \\& & 1 & & \\& & & \ddots & \\& & & & 1\end{array}\right]\right)^{-1} X^{T} y$